2.3. Mathematische Grundlagen

In diesem Abschnitt werden wir einige mathematische Grundlagen wiederholen, die in späteren Kapiteln nützlich sein werden, wie zum Beispiel bei der Fehleranalyse von linearen Gleichungssystemen. Hierbei wollen wir insbesondere verstehen wie sich Fehler in den Eingangsdaten von linearen Gleichungssystemen der Form \(Ax=b\) auswirken, d.h. bei Störungen des Vektors \(b\) und der Matrix \(A\). Dazu müssen wir die Fehler in vernünftiger Weise messen und benötigen daher also geeignete Normen.

2.3.1. Vektornormen

Da die Definition einer Vektornorm eines beliebigen Vektorraums \(V\) für alle folgenden Konzepte eine wichtige Rolle spielt wollen wir diese grundlegende Definition im Folgenden zunächst wiederholen.

Definition 2.6 (Vektornorm)

Sei \(V\) ein beliebiger Vektorraum über dem Körper \(\mathbb{K}\) der reellen oder komplexen Zahlen. Wir nennen eine Abbildung \(||\cdot|||\) von \(V\) in die nichtnegativen reellen Zahlen mit

\[\begin{aligned} ||\cdot|| \colon &V \rightarrow \mathbb{R}^+_0, \\ &x \mapsto ||x||, \end{aligned}\]

eine (Vektor-)Norm auf \(V\), wenn für alle Vektoren \(x,y \in V\) und alle Skalare \(\alpha \in \mathbb{K}\) die folgenden Axiome erfüllt sind:

1. \(||x|| = 0 \ \Rightarrow \ x = 0,\) (Definitheit)

2. \(||\alpha x|| = |\alpha| \cdot ||x||,\) (absolute Homogenität)

3. \(||x + y|| \leq ||x|| + ||y||.\) (Subadditivität)

Aus der Analysis kennen wir die obigen Eigenschaften einer Norm auf einem Vektorraum bereits und auch einige gängige Beispiele, die wir im Folgenden wiederholen werden.

Beispiel 2.7 (Vektornormen in endlichdimensionalen Räumen)

Betrachten wir Vektornormen auf dem endlichdimensionalen Vektorraum \(V \coloneqq \mathbb{R}^n\). Eine interessante Klasse von Vektornormen auf \(V\) ist durch die p-Normen gegeben für \(1 \leq p < \infty\) mit

\[\Vert x \Vert_p := \left( \sum_{i=1}^n \vert x_i \vert^p\right)^{1/p}.\]

Ein Spezialfall ist die Euklidische Norm für \(p=2\).

Darüber hinaus verwendet man auch häufig die sogenannte Maximumsnorm für \(p=\infty\) mit

\[\Vert x \Vert_\infty := \max_{1\leq i \leq n} \vert x_i \vert.\]

Unter den obigen Vektornormen hat die Euklidische Norm eine spezielle Rolle, da sie aus einem Skalarprodukt entsteht, nämlich

\[\langle x, y \rangle \ = \ \sum_{i=1}^n x_i y_i.\]

Ein Skalarprodukt, d.h. eine bilineare Abbildung mit \(\langle x, x \rangle > 0\) für \(x \neq 0\) induziert immer eine Norm durch

\[\Vert x \Vert \ \coloneqq \ \sqrt{\langle x, x \rangle} \ = \ \sqrt{\sum_{i=1}^n x_i^2}.\]

Dies vereinfacht viele Rechnungen im Vergleich zu allgemeinen Normen, typischerweise rechnet man dann mit dem Quadrat der Norm und verwendet die Eigenschaften das Skalarprodukts um einfache Relationen wie den Satz des Pythagoras zu erhalten. Man spricht in solchen Fällen von einem Hilbertraum. Der \(\mathbb{R}^n\) als normierter Raum hat die selben Elemente und topologisch äquivalente Normen, jedoch ist die Geometrie in der Interpretation eines Hilbertraums deutlich einfacher.

Ein grundlegendes Resultat ist die topologische Äquivalenz aller Normen in einem endlichdimensionalen Raum. Um also Konvergenzresultate zu beweisen ist es egal welche Norm wir verwenden. Wollen wir hingegen quantitative Abschätzungen, so besteht - insbesondere für den am meisten relevanten Fall von großer Dimension \(n\in \mathbb{R}^n\) - ein potentiell großer Unterschied zwischen den verschiedenen Normen. So gilt etwa die Abschätzung

\[\Vert x \Vert_\infty \leq \Vert x \Vert_1 \leq n \Vert x \Vert_\infty.\]

Im schlimmsten Fall ist also die \(1\)-Norm \(n\)-mal so groß wie die Maximumsnorm.

Bemerkung 2.3 (Wahl der Vektornorm)

In der Praxis ist es wichtig, welche Fehler man abschätzen möchte bzw. in den Eingabedaten abschätzen kann. Will man etwa garantieren, dass jeder Eintrag bis auf einen maximalen Fehler korrekt ist, muss man eine Abschätzung in der Maximumsnorm verwenden, während es für den mittleren Fehler reicht die \(1\)-Norm zu verwenden. Ähnliches gilt bei Eingabedaten, wenn man nur eine Schranke für jeden gemessenen Eintrag hat. In diesem Fall ist dies natürlich eine Schranke an die Maximumsnorm. Bei stochastischen Fehlern, die häufig auftreten, kommt man zu anderen Schranken. Ein Beispiel ist ein Modell der Form \(\tilde x_i = x_i + \epsilon_i\), mit Fehlern \(\epsilon_i\) die gleichverteilt, unabhängig sind und Mittelwert Null haben. Dann hat man üblicherweise eine Schranke an die Varianz, die bei großem \(n\) gut der empirischen Varianz, also dem Quadrat der Euklidischen Norm, entspricht.

2.3.2. Matrixnormen

Für eine Matrix kann man beliebige Normen definieren, etwa die Frobenius-Norm als Verallgemeinerung der Euklidischen Norm mit

\[\Vert A \Vert_F = \sqrt{\sum_{i,j} A_{ij}^2} .\]

Allerdings ist dabei nicht klar, wie der mathematische Zusammenhang zwischen Matrix- und Vektornorm aussieht. Insbesondere hätte man für einfache Abschätzungen gern eine Eigenschaft der Form

\[\Vert A x \Vert \ \leq \ \Vert A \Vert \cdot\Vert x \Vert,\]

wie sie auch im Eindimensionalen für den Betrag gelten. Deshalb ist es natürlich die Norm einer Matrix (oder auch die Norm linearer Operatoren, die im endlichdimensionalen isomorph zu den Matrizen sind) über folgende Relation in einem endlichdimensionalen Vektorraum \(V\) zu definieren

\[\Vert A \Vert \ \coloneqq \ \sup_{x \neq 0} \frac{\Vert A x\Vert}{\Vert x \Vert},\]

denn dann gilt schon automatisch

\[\frac{||Ay||}{||y||} \ \leq \ \sup_{x \neq 0} \frac{\Vert A x\Vert}{\Vert x \Vert} \ =: \ ||A|| \quad \Rightarrow \quad ||Ay|| \ \leq \ ||A|| \cdot ||y|| \quad \forall y\in V.\]

Wir müssen zunächst klären, dass wir damit eine Norm definiert haben und dass das Supremum auch endlich ist. Es ist auch zu beachten, dass in obiger Definition eigentlich zwei Normen vorkommen können: ist \(A \in \mathbb{R}^{m \times n}\) dann haben wir eine Norm in \(\mathbb{R}^n\) für \(x\) und eine Norm in \(\mathbb{R}^m\) für \(Ax\). Selbst im Fall \(m=n\) müssen diese nicht die Gleichen sein. Die folgende Definition deckt diesen allgemeinen Fall ab.

Definition 2.7 (Induzierte Operatornorm)

Seien \(V\) und \(W\) normierte Vektorräume mit den Normen \(\Vert \cdot \Vert_V\) bzw. \(\Vert \cdot \Vert_W\). Dann ist die induzierte Operatornorm eines linearen Operators \(A:V \rightarrow W\) definiert durch

(2.4)\[\Vert A \Vert \ \coloneqq \ \sup_{x \neq 0} \frac{\Vert A x\Vert_W}{\Vert x \Vert_V}.\]

Das folgende Beispiel zeigt häufig verwendete Matrixnormen.

Beispiel 2.8 (Matrixnormen)

Bei Matrixnormen betrachtet man vor allem jene, die von \(p\)-Normen im \(\R^n\) bzw. \(\R^m\) induziert sind, d.h.

\[\Vert A \Vert_{p,q} \ \coloneqq \ \sup_{x \neq 0} \frac{\Vert A x\Vert_p}{\Vert x \Vert_q}.\]

Besonders wichtig ist der Fall \(p=q\). Hier schreibt man einfach

\[\Vert A \Vert_{p} \coloneqq \sup_{x \neq 0} \frac{\Vert A x\Vert_p}{\Vert x \Vert_p}.\]

Hierbei sind wieder \(p=1,2,\infty\) die kanonischen Fälle. Wir werden in Beispiel 2.9 und Beispiel 2.10 sehen, dass man diese Matrixnormen in diesen Fällen auch einfacher charakterisieren kann.

Das folgende Theorem besagt, dass die induzierte Operatornorm für endlichdimensionale Vektorräume eine Vektornorm für Matrizen ist.

Satz 2.1 (Operatornorm für endlichdim. Vektorräume)

Seien \(V\) und \(W\) endlichdimensionale Vektorräume. Dann definiert (2.4) eine Vektornorm auf dem Raum der linearen Operatoren von \(V\) nach \(W\), der isomorph zum Raum der Matrizen \(\mathbb{R}^{m\times n}\) ist, wobei \(m= \dim(W) \in \mathbb{N}\) und \(n= \dim(V) \in \mathbb{N}\). Darüber hinaus gilt

(2.5)\[\Vert A x \Vert_W \ \leq \ \Vert A \Vert \cdot \Vert x \Vert_V.\]

Proof. Zunächst zeigen wir, dass das Supremum endlich ist, dazu verwenden wir, dass

\[\frac{\Vert A x\Vert_W}{\Vert x \Vert_V} \ = \ \Vert A y \Vert_W\]

gilt mit \(y\coloneqq\frac{x}{\Vert x \Vert_V}\), wobei \(\Vert y \Vert_V=1\). Also ist

\[\sup_{x \neq 0} \frac{\Vert A x\Vert_W}{\Vert x \Vert_V} \ = \sup_{\Vert y\Vert_V=1} \!\! \Vert Ay \Vert_W.\]

Nun suchen wir ein Supremum der stetigen Funktion \(y \mapsto \Vert Ay \Vert_W\) über der kompakten Einheitssphäre \(\{ y ~|~\Vert y \Vert_V = 1\}\) in \(V\). Damit ist dieses endlich und wird sogar als Maximum angenommen.

Nun müssen wir noch die drei Eigenschaften einer Norm nachweisen:

1. Per Definition ist \(\Vert A \Vert\) nichtnegativ und wir sehen \(\Vert 0 \Vert =0\). Ist nun umgekehrt \(\Vert A \Vert = 0\), so folgt sofort

   \[\sup_{x \neq 0} \frac{\Vert A x\Vert_W}{\Vert x \Vert_V} \ = \ 0\]

   und damit

   \[0 \ \leq \ \frac{\Vert A x\Vert_W}{\Vert x \Vert_V} \ \leq \ 0\]

   für alle \(x \in V\). Also folgt \(Ax = 0\) für alle \(x\) und somit muss schon \(A=0\) gelten.

2. Um absolute Homogenität zu erhalten benutzen wir für \(\alpha \in \R\)

   \[\Vert \alpha A \Vert = \sup_{x \neq 0} \frac{\Vert \alpha A x\Vert_W}{\Vert x \Vert_V} = \sup_{x \neq 0} \vert \alpha \vert~\frac{\Vert A x\Vert_W}{\Vert x \Vert_V} = \vert \alpha \vert~\sup_{x \neq 0} \frac{\Vert A x\Vert_W}{\Vert x \Vert_V} = \vert \alpha \vert~\Vert A \Vert.\]

3. Für die Dreiecksungleichung benutzen wir einfach die Dreiecksungleichung der Vektornorm in \(W\)

   \[\begin{aligned} \Vert A+B \Vert \ &= \ \sup_{x \neq 0} \frac{\Vert (A+B) x\Vert_W}{\Vert x \Vert_V} \ \leq \ \sup_{x \neq 0} \frac{\Vert Ax\Vert_W}{\Vert x \Vert_V} + \frac{\Vert Bx\Vert_W}{\Vert x \Vert_V}\\ \ &\leq \ \sup_{x \neq 0} \frac{\Vert Ax\Vert_W}{\Vert x \Vert_V} + \sup_{y \neq 0} \frac{\Vert By\Vert_W}{\Vert y \Vert_V}\\ \ &= \ \Vert A \Vert + \Vert B \Vert. \end{aligned}\]

(2.5) folgt direkt aus der Definition über das Supremum. ◻

Eine weitere interessante Eigenschaft einer induzierten Matrixnorm ist die Submultiplikativität.

Lemma 2.1 (Submultiplikativität)

Seien \(A:V\rightarrow W\) und \(B: U \rightarrow V\) lineare Operatoren. Dann gilt für die induzierten Operatornormen

\[\Vert A B \Vert \ \leq \ \Vert A \Vert \cdot \Vert B \Vert.\]

Proof. Dies sieht man leicht aus der Identität

\[\frac{\Vert A B x\Vert_W}{\Vert x \Vert_U} \ = \ \frac{\Vert A B x\Vert_W}{\Vert B x \Vert_V} \frac{\Vert B x\Vert_V}{\Vert x \Vert_U}\]

falls \(Bx \neq 0\). Damit folgt sofort die Abschätzung für das Supremum mit

\[\Vert A B \Vert \ = \ \sup_{x \neq 0}\frac{\Vert A B x\Vert_W}{\Vert B x \Vert_V} \frac{\Vert B x\Vert_V}{\Vert x \Vert_U} \ \leq \ \sup_{y \neq 0}\frac{\Vert A y\Vert_W}{\Vert y \Vert_V} \sup_{x \neq 0} \frac{\Vert B x\Vert_V}{\Vert x \Vert_U} \ = \ \Vert A \Vert \cdot \Vert B \Vert.\]

◻

Wir erwähnen noch eine natürliche Eigenschaft der induzierten Matrixnorm. Die Norm der Einheitsmatrix in \(\R^{n \times n}\) ist für eine induzierte Matrixnorm mit \(V=W\) immer gleich \(1\).

Zum Abschluss machen wir noch einige Beispiele, die Matrixnormen genauer charakterisieren. Wir beginnen mit der sogenannten Zeilensummennorm.

Beispiel 2.9 (Zeilensummennorm)

Wir beginnen mit dem Fall \(p=q=\infty\). Es gilt per Definition

\[\Vert A \Vert_\infty \ = \ \sup_{x\neq 0} \frac{\max_j \vert \sum_k A_{jk} x_k \vert}{\max_i \vert x_i \vert}.\]

Wir beginnen mit einer einfachen Abschätzung nach oben. Es gilt für jedes \(j = 1,\ldots,n\)

\[\left\vert \sum_k A_{jk} x_k \right\vert \ \leq \ \sum_k \vert A_{jk} \vert \cdot \vert x_k \vert \ \leq \ \sum_k \vert A_{jk} \vert \cdot \max_i \vert x_i \vert.\]

Daraus folgt schon

\[\Vert A \Vert_\infty \ = \ \sup_{x\neq 0} \frac{\max_j \vert \sum_k A_{jk} x_k \vert}{\max_i \vert x_i \vert} \ \leq \ \sup_{x\neq 0} \frac{ \max_j \sum_k \vert A_{jk} \vert \cdot \max_i \vert x_i \vert}{\max_i \vert x_i \vert} \ = \ \max_j \sum_k \vert A_{jk} \vert.\]

Nun wollen wir zeigen, dass sogar Gleichheit gilt. Dazu betrachten wir ein spezielles \(x\). Sei \(\ell \in \lbrace1, \ldots, n \rbrace\) so, dass

\[\sum_k \vert A_{\ell k} \vert \ = \ \max_j \sum_k \vert A_{jk} \vert.\]

Dann wählen wir den Vektor \(\overline{x}_k \coloneqq \text{sgn}(A_{\ell k})\) und erhalten

\[\Vert A \Vert_\infty \ = \ \sup_{x\neq 0} \frac{\max_j \vert \sum_k A_{jk} x_k \vert}{\max_i \vert x_i \vert} \ \geq \ \frac{\max_j \vert \sum_k A_{jk} \overline{x}_k \vert}{\max_i \vert \overline{x}_i \vert} .\]

Da offensichtlich aus der Wahl von \(\overline{x}\) folgt \(\max_i \vert \overline{x}_i \vert = 1\), gilt

\[\Vert A \Vert_\infty \geq \max_j \vert \sum_k A_{jk} \overline{x}_k \vert \geq \vert \sum_k A_{\ell k} \overline{x}_k \vert = \ \sum_k \vert A_{\ell k} \vert \ = \ \max_j \sum_k \vert A_{jk} \vert.\]

Wir haben also gezeigt, dass die folgende Gleichung gilt:

\[\Vert A \Vert_\infty \ = \ \max_j \sum_k \vert A_{jk} \vert\]

Dies ist deutlich einfacher zu berechnen als die ursprüngliche Definition über das Supremum. Man nennt diese Norm aus offensichtlichen Gründen auch Zeilensummennorm.

Darüber hinaus wollen wir die wichtige Spektralnorm im Folgenden näher charakterisieren.

Beispiel 2.10 (Spektralnorm)

Nun betrachten wir die von der Euklidischen Norm induzierte Matrixnorm, d.h. \(p=q=2\). Wie immer im Fall der Euklidischen Norm ist es einfacher mit dem Quadrat der Norm zu rechnen, wir betrachten also

\[\frac{\Vert A x \Vert_2^2}{\Vert x \Vert^2} \ = \ \frac{\langle Ax, Ax \rangle}{\langle x, x \rangle} \ = \ \frac{x^T A^T A x}{x^T x }.\]

Die Matrix \(A^T A\) ist symmetrisch und positiv semidefinit, also existiert gemäß Satz 2.3 eine Diagonalisierung der Form \(A^T A = Q D Q^T\) mit einer orthogonalen Matrix \(Q\) und einer Diagonalmatrix \(D\) aus nichtnegativen Eigenwerten von \(A^T A\). Es gilt also

\[x^T A^T A x \ = \ x^T Q D Q^T x, \qquad x^T x \ = \ x^T Q Q^T x.\]

Definieren wir nun einen Vektor \(y=Q^T x\), so folgt sofort

(2.6)\[\Vert A \Vert_2^2 \ = \ \sup_{x\neq 0} \frac{\Vert A x \Vert_2^2}{\Vert x \Vert^2} \ = \ \sup_{y\neq 0} \frac{y^T D y}{y^T y}.\]

Ist nun \(d \in \mathbb{R}^+_0\) der größte Eintrag in \(D\), so folgt \(y^T D y \leq d y^T y\) und eingesetzt in (2.6) somit auch \(\Vert A \Vert_2^2 \leq d.\)

Andererseits können wir \(\overline{y}\) als einen Einheitsvektor wählen, der den Eintrag \(1\) in der selben Zeile hat wie der Eintrag \(d\) in der Matrix \(D\). Also ist

\[\Vert A \Vert_2^2 \ = \ \sup_{y\neq 0} \frac{y^T D y}{y^T y} \ \geq \ \frac{\overline{y}^T D \overline{y}}{\overline{y}^T \overline{y}} \ = \ d.\]

Also haben wir gezeigt, dass wir die sogenannte Spektralnorm einer Matrix berechnen können als

\[\Vert A \Vert_2 \ = \ \sqrt{\lambda_{\max}(A^T A)},\]

wobei \(\lambda_{\max}(A^T A) =: d\) den größten Eigenwert von \(A^T A\) bezeichnet.

Eine wichtige Größe im Zusammenhang mit Matrixnormen ist auch der Spektralradius einer quadratischen Matrix \(A \in \R^{n \times n}\), der gegeben ist durch

\[\rho(A) \ \coloneqq \ \max\{|\lambda|~|~\lambda \text{ ist Eigenwert von } A\}.\]

Es gilt offensichtlich für jede Matrixnorm

\[\Vert A \Vert \ \geq \ \frac{\Vert A x_\lambda\Vert}{\Vert x_\lambda \Vert} \ = \ \frac{\Vert \lambda x_\lambda \Vert}{\Vert x_\lambda \Vert} \ = \ \vert \lambda \vert \cdot \frac{\Vert x_\lambda \Vert}{\Vert x_\lambda \Vert} \ = \ \vert\lambda\vert,\]

wobei \(x_\lambda \in \R^n\) der zugehörige Eigenvektor zu \(\lambda\) ist. Damit ist der Spektralradius eine untere Schranke für jede Matrixnorm.

Ist \(A\) eine symmetrische Matrix, so gilt sogar nach Beispiel 2.10 \(\rho(A)=\Vert A \Vert_2 = \sqrt{\lambda_{\max}(A^T A)}\), da der betragsmäßig größte Eigenwert von \(A^T A = A^2\) gleich dem Quadrat des betragsmäßig größten Eigenwerts von \(A\) ist.

Bemerkung 2.4

Allgemeiner gilt, dass für jede Matrix \(A\) und jedes \(\epsilon > 0\) eine Matrixnorm existiert, so dass \(\Vert A \Vert < \rho(A) + \epsilon\) ist.

2.3.3. Konditionszahl einer Matrix

Eine wichtige Kennzahl für eine invertierbare Matrix ist die sogenannte Konditionszahl, die wir im Folgenden definieren werden.

Definition 2.8 (Konditionszahl)

Sei \(A \in \mathbb{R}^{n \times n}\) eine invertierbare Matrix und \(||\cdot||\) eine zugeordnete Matrixnorm. Dann ist die (relative) Konditionszahl der Matrix \(A\) definiert als:

\[\kappa(A) \ \coloneqq \ \Vert A \Vert \cdot \Vert A^{-1} \Vert.\]

Aus obiger Definition wird klar, dass die Konditionszahl \(\kappa(A)\) einer Matrix \(A\) direkt von der gewählten Matrixnorm abhängt. Für \(p\)-Normen schreiben wir deshalb auch

\[\kappa_p(A) \ \coloneqq \ \Vert A \Vert_p \cdot \Vert A^{-1} \Vert_p.\]

Unabhängig von der Matrixnorm gilt immer \(\kappa(I) =1\) und wegen der Submultiplikativität für induzierte Matrixnormen aus Lemma 2.1 erhalten wir

\[\kappa(A) \ = \ \Vert A \Vert \cdot \Vert A^{-1} \Vert \ \geq \ \Vert A A^{-1} \Vert \ = \ \Vert I \Vert \ = \ 1.\]

Wir sehen also, dass die Konditionszahl immer größer oder gleich eins ist und bei der Einheitsmatrix ihr Minimum annimmt.

Wie wir später sehen werden ist die Konditionszahl ein entscheidendes Stabilitätsmaß für die Lösung linearer Gleichungssysteme.

2.3.4. Neumannsche Reihe

Betrachten wir Störungen einer regulären Matrix, so stellt sich immer die Frage, ob die gestörte Matrix dann noch regulär ist. Ist \(A \in \mathbb{R}^{n \times n}\) eine reguläre Matrix und \(\Delta_A \coloneqq \tilde{A} - A \in \mathbb{R}^{n \times n}\) eine Störung von \(A\), so gilt offensichtlich

\[\tilde{A} = A + \Delta_A \ = \ A\ (I + A^{-1}\Delta_A).\]

Da wir \(A\) als regulär angenommen haben ist die Matrix \(\tilde A\) also genau dann regulär, wenn die Matrix \(I + A^{-1}\Delta_A = I - B\) mit \(B \coloneqq -A^{-1}\Delta_A\) regulär ist. Diese lässt sich auch als eine Störung der Einheitsmatrix auffassen. Das heißt wir müssen diese Frage nur für die Einheitsmatrix beantworten und somit verstehen unter welcher Bedingung an die Störung \(B \in \mathbb{R}^{n \times n}\) wir garantieren können, dass \(I-B\) noch regulär ist.

Für ein besseres Verständnis betrachten wir zunächst den eindimensionalen Fall für \(n=1\). Man sieht ein, dass die Zahl \((1-b) \in \R\) invertierbar ist (also ungleich Null sein muss), wenn \(b \neq 1\) gilt. Darüber hinaus wissen wir aus der Analysis, dass für die stärkere Bedingung \(\vert b \vert < 1\) gilt, dass die folgende geometrische Reihe absolut konvergiert mit

\[\sum_{k=0}^\infty b^k \ = \ \frac{1}{1-b} \ = \ (1 - b)^{-1}.\]

Diese Beobachtung motiviert eine analoge Aussage im höherdimensionalen Matrix-Fall, was uns zum Konzept der sogenannten Neumannschen Reihe führt.

Satz 2.2 (Konvergenz der Neumannschen Reihe)

Sei \(B \in \mathbb{R}^{n \times n}\) mit \(\Vert B \Vert < 1\). Dann konvergiert die Neumannsche Reihe

\[S_n \ \coloneqq \ \sum_{k=0}^n B^k\]

für \(n \rightarrow \infty\) absolut und es gilt \(\lim_{n \rightarrow \infty} S_n = (I-B)^{-1}\).

Insbesondere ist \(I-B\) somit invertierbar und es gilt außerdem die Abschätzung

\[\left\| (I-B)^{-1} \right\| \ \leq \ \frac{1}{1-\Vert B \Vert}.\]

Proof. Wir zeigen zunächst, dass \((S_n)_{n\in\mathbb{N}}\) eine Cauchy-Folge ist. Es gilt für \(m > n\) wegen der Dreiecksungleichung

\[\norm{ S_m - S_n } \ = \ \norm{\!\!\! \sum_{k=n+1}^m \!\!\!B^k } \ \leq \sum_{k=n+1}^m \lVert B^k \rVert.\]

Auf Grund der Submultiplikativität der Matrixnorm folgern wir direkt \(\Vert B^k \Vert \leq \Vert B \Vert^k\) und somit erhalten wir insgesamt

\[\Vert S_m - S_n \Vert \ \leq \ \sum_{k=n+1}^m \lVert B \rVert^k \ = \ \Vert B \Vert^{n+1} \cdot \!\!\!\! \sum_{k=0}^{m-(n+1)} \!\!\! \Vert B \Vert^k \ \leq \ \Vert B \Vert^{n+1} \sum_{k=0}^{\infty} {\underbrace{\Vert B \Vert}_{<\, 1}}^k \ = \ \frac{\Vert B \Vert^{n+1} }{1-\Vert B \Vert}.\]

Da \(\Vert B \Vert < 1\) ist, konvergiert die rechte Seite für \(n \rightarrow \infty\) unabhängig von \(m\) absolut gegen Null, d.h. \(S_n\) ist eine Cauchy-Folge.

Betrachten wir nun den Grenzwert der Folge \((S_n)_{n\in \mathbb{N}}\). Es gilt folgende nützliche Identität

\[S_n(I - B) \ = \ S_n - \sum_{k=0}^n B^{k+1} \ = \ I-B^{n+1} = (I-B) S_n.\]

Wir nutzen nun aus, dass \(B^{n+1}\) gegen die Nullmatrix konvergiert und verwenden die obige Gleichung um zu zeigen, dass sowohl eine Links- und eine Rechtsinverse zur Matrix \((I - B)\) existieren und dass diese übereinstimmen:

\[\begin{aligned} &S_\infty (I-B) \ = \ \lim_{n\rightarrow\infty} \sum_{k=0}^n B^k (I-B) \ = \ % \lim_{n\rightarrow\infty} \sum_{k=0}^n B^k - \sum_{k=1}^{n+1} B^k \ = \ % \lim_{n\rightarrow\infty} I - B^{n+1}\\ % \ = \ & I\\ % \ = \ &\lim_{n\rightarrow\infty} I - B^{n+1} \ = \ \lim_{n\rightarrow\infty} \sum_{k=0}^n B^k - \sum_{k=1}^{n+1} B^k \ = \ % (I-B) \lim_{n\rightarrow\infty} \sum_{k=0}^n B^k \ = \ % % (I-B) S_\infty. \end{aligned}\]

Daraus folgt also schon direkt, dass

\[S_\infty \ = \ \lim_{n\rightarrow \infty} S_n \ = \ (I - B)^{-1}.\]

Zuletzt zeigen wir noch die Abschätzung des Theorems. Wegen der Voraussetzung \(||B|| < 1\) und

\[\Vert S_n \Vert \ = \ \norm{ \sum_{k=0}^n B^k } \ \leq \ \sum_{k=0}^n \Vert B^k \Vert \ \leq \ \sum_{k=0}^\infty \Vert B^k \Vert \ \leq \ \sum_{k=0}^\infty \Vert B \Vert^k \ = \ \frac{1}{1-\Vert B \Vert}\]

erhalten wir die Abschätzung

\[\left\| (I - B)^{-1} \right\| \ = \ ||S_\infty|| \ = \ \left\Vert \lim_{n\rightarrow \infty} S_n \right\Vert \ \leq \ \frac{1}{1-||B||}.\]

◻

2.3.5. Singulärwertzerlegung

Eine weitere nützliche Technik bei der Fehleranalyse linearer Probleme ist die Singulärwertzerlegung einer Matrix. Wir erinnern zunächst an die aus der linearen Algebra bekannte Diagonalisierung symmetrischer Matrizen.

Satz 2.3 (Diagonalisierung)

Sei \(B \in \R^{n \times n}\) eine symmetrische Matrix, d.h. \(B=B^T\). Dann existiert eine orthogonale Matrix \(Q \in \R^{n \times n}\), deren Spalten aus den Eigenvektoren von \(B\) bestehen und eine Diagonalmatrix \(D \in \R^{n \times n}\), deren Einträge die Eigenwerte von \(B\) sind, so dass gilt:

\[B \ = \ Q D Q^T.\]

Proof. Siehe [FS20]. ◻

Eine andere Version die Diagonalisierung zu schreiben bezieht sich auf das Matrix-Vektorprodukt, denn es gilt

\[B x \ = \ QDQ^T x \ = \ Q D \begin{pmatrix} \langle u_1, x \rangle \\ \vdots \\ \langle u_n, x \rangle \end{pmatrix} \ = \ Q \begin{pmatrix} \lambda_1 \langle u_1, x \rangle \\ \vdots \\ \lambda_n \langle u_n, x \rangle \end{pmatrix} \ = \ \sum_{j=1}^n \lambda_j \langle u_j, x \rangle u_j.\]

wobei \(\lambda_j\) die Eigenwerte und \(u_j\) die zugehörigen Eigenvektoren der Matrix \(B\) sind für \(j=1,\ldots,n\).

Für allgemeinere \(n \times n\) Matrizen gilt im Allgemeinen kein solches Resultat, da die Eigenvektoren im Allgemeinen keine Orthonormalbasis bilden. Für nichtquadratische Matrizen sind Eigenwertprobleme gar nicht erst definiert. Deshalb verallgemeinert man bei der Singulärwertzerlegung einer Matrix \(A \in \R^{m \times n}\) die Definition auf Singulärvektoren \(u_i \in \R^n\) und \(v_i \in \R^m\). Um diese zu konstruieren betrachten wir die beiden symmetrischen, positiv semidefiniten Matrizen

\[B_1 \coloneqq A^T A \in \R^{n \times n}, \qquad B_2 \coloneqq A A^T \in \R^{m \times m}.\]

Diese sind nach Satz 2.3 diagonalisierbar, d.h. es gibt eine Orthonormalbasis aus Eigenvektoren, so dass man orthogonale Matrizen \(U \in \mathbb{R}^{n\times n}\), \(V\in \mathbb{R}^{m\times m}\) und Diagonalmatrizen \(D_1 \in \mathbb{R}^{n\times n}\), \(D_2 \in \mathbb{R}^{m\times m}\) erhält, so dass folgendes gilt

\[B_1 = U D_1 U^T, \qquad B_2 = V D_2 V^T.\]

Bemerkung 2.5

Zwischen den Eigenwerten der beiden Matrizen \(B_1\) und \(B_2\) besteht ein interessanter Zusammenhang. Sei \(\lambda_i \neq 0\) ein beliebiger Eigenwert von \(B_1\) mit Eigenvektor \(u_i\), dann gilt wegen der Eigenwertgleichung

\[B_2 A u_i \ = \ AA^T A u_i \ = \ AB_1 u_i \ = \ \lambda_i A u_i.\]

Dementsprechend ist \(\lambda_i\) auch Eigenwert von \(B_2\) mit Eigenvektor \(v_i := Au_i\). Umgekehrt kann man auch zeigen, dass jeder Eigenwert von \(B_2\) auch Eigenwert von \(B_1\) ist. Wir beachten weiter, dass für die Euklidische Norm dieses Eigenvektors \(v_i\) gilt:

\[\Vert v_i \Vert_2 \ = \ \Vert A u_i \Vert_2 \ = \ \sqrt{\langle A u_i, A u_i \rangle} \ = \ \sqrt{u_i^T A^T A u_i}\ = \ \sqrt{u_i^T B_1 u_i} \ = \ \sqrt{\lambda_i u_i^T u_i} \ = \ \sqrt{\lambda_i}.\]

Aus obiger Beobachtung können wir nun sinnvoll die Singulärwertzerlegung einer nicht-quadratischen Matrix \(A \in \mathbb{R}^{m \times n}\) definieren.

Definition 2.9 (Singulärwertzerlegung)

Sei \(A \in \mathbb{R}^{m \times n}\) eine reelle Matrix mit Rang \(r \in \mathbb{N}\) mit \(r \leq \min \lbrace m,n \rbrace\). Dann bezeichnen wir ein Matrixprodukt der Gestalt

\[A \ = \ U \Sigma V^T,\]

als Singulärwertzerlegung (SVD) von \(A\), wenn \(U \in \mathbb{R}^{m\times m}\) und \(V \in \mathbb{R}^{n \times n}\) orthogonale Matrizen sind und \(\Sigma \in \mathbb{R}^{m \times n}\) eine Diagonalmatrix ist, deren erste \(r\) Einträge positive, reelle Werte \(\sigma_1, \ldots, \sigma_r\) enthält und sonst nur aus Nullen besteht.

Wir nennen die positiven Diagonaleinträge \(\sigma_i, i=1,\ldots,r\) Singulärwerte der Matrix \(A\) und es lässt sich leicht zeigen, dass \(\sigma_i = \sqrt{\lambda_i}\) gilt, wobei \(\lambda_i\) Eigenwert von \(A^TA\) ist für \(i=1,\ldots,r\).

Die Spaltenvektoren der Matrizen \(U\) und \(V\) nennen wir links- bzw. rechts-Singulärvektoren.

Bemerkung 2.6 (Gestalt der Singulärwertzerlegung)

Für \(A\in\R^{m\times n}, m>n\) hat die Singulärwertzerlegung von \(A\) mit \(A = U \Sigma V^T\) dann folgende Form,

\[\begin{aligned} A = \begin{pmatrix} U_{11} & \ldots & U_{1m}\\ \vdots & & \vdots\\ U_{m1} & \ldots & U_{mm}\\ \end{pmatrix} \begin{pmatrix} \sigma_1 & & \\ & \ddots & & \\ & & \sigma_r\\ & & & 0\\ & & & & \ddots\\ & & & & & 0\\ 0& & & \ldots & & 0\\ \vdots& & & \ldots & & \vdots\\ 0& & & & & 0\\ \end{pmatrix} \begin{pmatrix} V_{11} & \ldots & V_{n1}\\ \vdots & & \vdots\\ V_{1n} & \ldots & V_{nn} \end{pmatrix}. %\begin{pNiceMatrix}[margin] %\Block[fill=blue!15]{3-3}{ } %U_{11} & \ldots & U_{1m}\\ %\vdots & & \vdots\\ %U_{m1} & \ldots & U_{mm}\\ %\end{pNiceMatrix} %\begin{pNiceMatrix}[margin] %\Block[fill=green!15]{3-3}{ } %\sigma_1 & & \\ %& \ddots & & \\ %& & \sigma_r\\ %& & & 0\\ %& & & & \ddots\\ %& & & & & 0\\ %0& & & \ldots & & 0\\ %\vdots& & & \ldots & & \vdots\\ %0& & & & & 0\\ %\end{pNiceMatrix} %\begin{pNiceMatrix}[margin] %\Block[fill=yellow!15]{3-3}{ } %V_{11} & \ldots & V_{n1}\\ %\vdots & & \vdots\\ %V_{1n} & \ldots & V_{nn} %\end{pNiceMatrix}. \end{aligned}\]

Eine andere Version die SVD zu schreiben bezieht sich auf das Matrix-Vektorprodukt, denn es gilt

\[A x \ = \ \sum_{j=0}^n \sigma_j \langle u_j, x\rangle v_j.\]

Wegen der Eigenschaften der orthogonalen Matrizen \(U\) und \(V\) können wir hieraus sofort folgern, dass die folgenden Gleichungen für die Singulärvektoren gelten

\[A^T u_i \ = \ \sigma_i v_i, \qquad A v_i \ = \ \sigma_i u_i.\]

Beispiel 2.11 (Scherung)

Wir betrachten die Scherungsmatrix

\[\begin{aligned} M = \begin{pmatrix} 1 & m\\ 0 &1 \end{pmatrix} \end{aligned}\]

zu einem Parameter \(m\in\R\). Wir betrachten im Folgenden Punkte im Einheitskreis \(x\in B_1(0)\) und dazu die Singulärwertzerlegung \(M = U\Sigma V^T\) von \(M\).

In fig:svd bilden wir die Effekte der einzelnen Teilmatrizen für \(m=1\) angewendet auf \(x\in B_1(0)\) ab. In diesem Fall gilt für die Matrix \(\Sigma\) der Singulärwerte von \(M\)

\[\begin{aligned} \Sigma = \begin{pmatrix} \phi & 0\\ 0 & 1/\phi \end{pmatrix} \end{aligned}\]

wobei \(\phi= (1+\sqrt{5})/2\) der goldene Schnitt ist. Diesen Wert erhält man hier nur speziell für \(m=1\). Die orangen Pfeile zeigen am Anfang auf \(e_1 = (1,0)\) und \(e_2 = (0,1)\). Die goldenen Pfeile in (c) zeigen auf die maximale Ausdehnung in \(x\) und \(y\) Richtung und haben die jeweils die Längen \(\sigma_1 = \Phi\) und \(\sigma_2 = 1 / \Phi\).

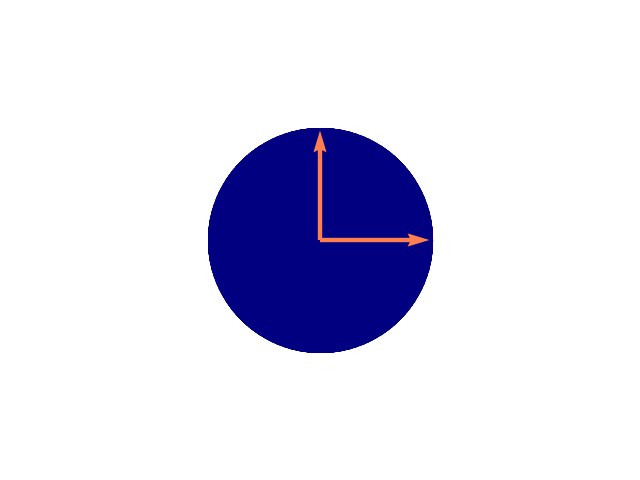
Abb. 2.1 \(B_1(0)\).

Abb. 2.2 \(V^T B_1(0)\).

Abb. 2.3 \(\Sigma\ V^T B_1(0)\).

Abb. 2.4 \(U\ \Sigma\ V^T B_1(0)\).