2.5. Kondition eines Problems und Stabilität von Verfahren

Bei der Fehleranalyse numerischer Verfahren betrachtet man typischerweise zwei verschiedene Fehlerquellen:

• die Kondition eines mathematisches Problems, d.h. wir betrachten die exakte Lösung eines Problems und untersuchen, wie sich Störungen auf diese Lösung auswirken,

• die Stabilität eines numerischen Verfahrens, d.h. wir approximieren bewusst die Lösung eines mathematisches Problem numerisch und untersuchen ob dieses Verfahren gegen die echte Lösung konvergiert.

In den folgenden beiden Abschnitten wollen wir die wichtigsten Konzepte dieser beiden Fehleranalysen einführen.

2.5.1. Kondition und Verstärkungsfaktoren

Im Folgenden erweitern wir die Definition der Konditionszahl einer Matrix in Definition 2.8 auf die Kondition allgemeiner mathematischer Probleme. Abstrakt können wir die Lösung eines mathematischen Problems meist als Funktion zwischen (normierten) Vektorräumen interpretieren, die gegebene Daten \(d\) auf eine Lösung \(x\) abbildet, d.h. \(x=f(d)\). Wir interessieren uns im Folgenden insbesondere für die Änderungen des Ergebnisses \(f(d)\) bei Störungen von \(d\).

Definition 2.10 (Kondition eines mathematischen Problems)

Seien \(V,W\) zwei normierte Vektorräume, \(f \colon V \rightarrow W\) eine Funktion und sei \(\delta > 0\) die maximale Größe relevanter Störungen. Dann definieren wir die Kondition des mathematischen Problems \(x = f(d)\) mit Daten \(d\) und Lösung \(x\) als den größtmöglichen relativen Fehler bei Störungen der Größe \(\delta\) als

\[\begin{aligned} \kappa(f;d) \ \coloneqq \ \sup_{\Vert \Delta_d \Vert \leq \delta} \frac{\Vert f(d+\Delta_d) -f(d) \Vert}{\Vert f(d) \Vert} \cdot \frac{\Vert d \Vert}{\Vert \Delta_d \Vert}. \end{aligned}\]

Im Folgenden wollen wir die obige Definition der Kondition eines mathematischen Problems auf den schon bekannten Fall der Lösung eines linearen Gleichungssystems anwenden.

Beispiel 2.12 (Lösung eines linearen Gleichungssystems)

Wir betrachten die Lösung des linearen Gleichungssystems \(Ax = b\) für \(A \in \R^{n \times n}\) und \(x,b \in \R^n\). Also nach der Notation in Definition 2.10 setzen wir \(x=A^{-1}b = f(d)\) mit den gegebenen Daten \(b=d\). Dann gilt

\[\begin{split} \kappa(A;b) \ &= \ \sup_{\Vert \Delta_d \Vert \leq \delta} \frac{\Vert A^{-1}(b + \Delta_b) - A^{-1}b\Vert \cdot \Vert b \Vert}{\Vert A^{-1}b \Vert \cdot \Vert \Delta_b\Vert}\\ \ &= \ \sup_{\Vert \Delta_b \Vert \leq \delta} \frac{\Vert A^{-1}\Delta_d\Vert \cdot \Vert b \Vert}{\Vert A^{-1}b \Vert \cdot \Vert \Delta_d\Vert} \ = \ \Vert A^{-1} \Vert \cdot \frac{\Vert b \Vert}{\Vert A^{-1}b \Vert}. \end{split}\]

Die Zahl \(\kappa(A;b)\) misst also die lokale Kondition bei der Lösung mit Störung von \(b\). Wollen wir ein globales Maß, so können wir noch den schlechtest möglichen Fall betrachten, d.h. das Supremum des Fehlers oben. Dann gilt

\[\begin{aligned} \sup_{b \in \R^n} \kappa(A;b) \: = \: \sup_{b \in \R^n} \Vert A^{-1} \Vert \cdot \frac{\Vert b \Vert}{\Vert A^{-1}b \Vert} \: = \: \Vert A^{-1} \Vert \cdot \sup_x \frac{\Vert Ax \Vert}{\Vert x \Vert} \: = \: \Vert A^{-1} \Vert \cdot \Vert A \Vert \: = \: \kappa(A). \end{aligned}\]

In diesem Sinne ist unsere Definition also auch konsistent mit der Konditionszahl einer Matrix aus Definition 2.8.

Wir erkennen aber auch, dass die Matrix-Konditionszahl \(\kappa(A)\) deutlich gröber ist, als die Problem-Kondition \(\kappa(A;b)\). Dazu plotten wir in fig:relerror die beiden Größen für die quadratische Matrix

\[\begin{aligned} A = \begin{pmatrix} 1 & 1\\ 0 & 2 \end{pmatrix} \end{aligned}\]

über die Menge der Vektoren \(b\in [0,1]^2 \subset \R^2\). Wir erkennen, dass der Wert \(\kappa(A;b)\) meist deutlich unter \(\kappa(A)\) liegt. In (a) und (b) plotten wir \(\frac{\norm{b}}{\norm{A^{-1}b}}\) über \(b\) und die gelbe Linie im Konturplot zeigt die Richtung des zugehörigen Links-Singulärvektors des größten Singulärwerts von \(A^{-1}\) an. Wir erkennen, dass der Wert von \(\kappa(A;b)\) gerade für diese Vektoren maximal wird. In (c) plotten wir \(\frac{\norm{Ax}}{\norm{x}}\) über \(x\) und die gelbe Linie im Konturplot zeigt die Richtung des zugehörigen Links-Singulärvektors des größten Singulärwerts von \(A\) an.

Bemerkung 2.7 (Zusammenhang zwischen SVD und Spektralnorm)

Es sei \(A\in\R^{m \times n}\) eine Matrix mit der Singulärwertzerlegung \(A=U\Sigma V^T\) und \(r\leq\min(m,n)\) absteigend geordneten Singulärwerten. Wir sehen, dass

\[\begin{aligned} \norm{Ax}_2 \: &= \: \langle Ax,Ax\rangle \: = \: \langle A^TAx,x\rangle \: = \: \langle V\Sigma^T U^TU\Sigma V^T x,x\rangle \: = \: \langle V \Sigma_n^2 V^T x,x\rangle\\ \: &= \: \langle \Sigma^2 V^T x,V^T x\rangle \: = \: \sum_{i=1}^r \sigma_i^2 \langle v_i, x \rangle^2. \end{aligned}\]

Da wir die Singulärwerte \(\sigma_1 \geq \ldots \sigma_r\) als absteigend sortiert angenommen haben, folgt dann

\[\begin{aligned} \norm{A}_2 \: = \: \sup_{\norm{x}_2=1} \norm{Ax}_2 \: = \: \sigma_1 \langle v_1, v_1 \rangle \: = \: \sigma_1. \end{aligned}\]

Dies bedeutet einerseits, dass die Spektralnorm durch den größten Singulärwert gegeben ist und andererseits, dass das Supremum in der Spektralnorm gerade für den zugehörigen Rechts-Singulärvektor \(v_1 \in \R^n\) angenommen wird.

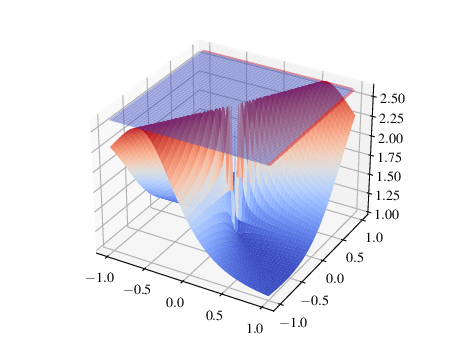
Abb. 2.5 Oberfläche von \(\frac{\norm{b}}{\norm{A^{-1}b}}\).

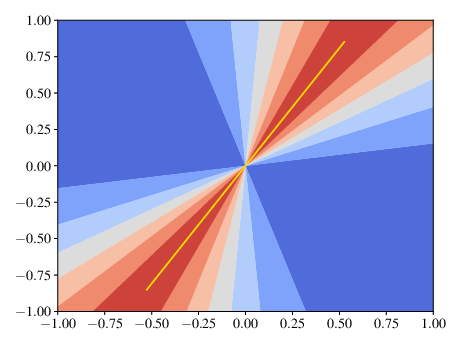
Abb. 2.6 Niveaumengen von \(\frac{\norm{b}}{\norm{A^{-1}b}}\).

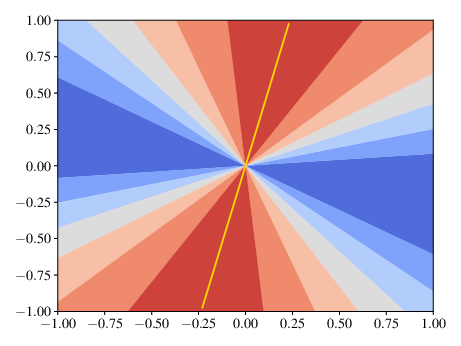
Abb. 2.7 Niveaumengen von \(\frac{\norm{Ax}}{\norm{x}}\).

Da wir im Allgemeinen von kleinen Störungen \(\Delta_d\) ausgehen, können wir die Kondition eines mathematischen Problems auch lokal mittels einer Taylor-Approximation beschreiben. Ist die Funktion \(f:\R^n\to\R^m\) stetig differenzierbar, so gilt bekanntermaßen

\[\begin{aligned} f(d+\Delta_d) -f(d) \ = \ f'(\Delta_d) d + o(\delta). \end{aligned}\]

Unter Vernachlässigung des Terms höherer Ordnung erhalten wir die sogenannten Verstärkungsfaktoren.

Definition 2.11 (Verstärkungsfaktor)

Es sei \(f:\R^n\to\R^m\) eine stetig differenzierbare Funktion und \(\delta > 0\) die maximale Größe relevanter Störungen. Dann definieren wir den Verstärkungsfaktor von \(f\) mit Hilfe der Jacobi-Matrix \(Df(d) \in \R^{m \times n}\) für gegebene Daten \(d \in \R^n\) durch:

\[\begin{aligned} V(f; d) \ \coloneqq \ \sup_{\norm{\Delta_d} \leq \delta} \frac{\norm{Df(d)\Delta_d}}{\norm{f(d)}} \cdot \frac{\norm{d}}{\norm{\Delta d}}. \end{aligned}\]

Damit berechnen wir nichts anderes als die zugeordnete Matrixnorm der Jacobi-Matrix \(Df(d)\) und erhalten somit schließlich

(2.9)\[V(f;d) \ = \ \sup_{\norm{\Delta_d} \leq \delta} \frac{\norm{Df(d)\Delta_d}}{\norm{\Delta d}} \cdot \frac{\norm{d}}{\norm{f(d)}} \ = \ \frac{\Vert Df(d) \Vert\cdot\Vert d \Vert}{\Vert f(d) \Vert}.\]

Bemerkung 2.8

Für Probleme \(f(b) = A^{-1} b\) zur Lösung eines linearen Gleichungssystems mit einer quadratischen Matrix \(A\in\R^{n,n}\) gilt offensichtlich \(Df(d) \equiv A^{-1}\) und somit erhält man den Verstärkungsfaktor

\[\begin{aligned} V(f; b) \: = \: \frac{\norm{A^{-1}}\cdot\norm{b}}{\norm{A^{-1} b}} \: = \: \norm{A^{-1}}\cdot \frac{\norm{b}}{\norm{A^{-1} b}} \: = \: \kappa(f;b). \end{aligned}\]

Dies passt zur Intuition, dass der Verstärkungsfaktor eine Taylorapproximation erster Ordnung an die Kondition eines Problems ist.

Im folgenden Beispiel wollen wir die Rolle der Verstärkungsfaktoren am Beispiel quadratischer Gleichungen untersuchen.

Beispiel 2.13 (Lösung von quadratischen Gleichungen)

Als Beispiel zur Berechnung des Verstärkungsfaktors eines mathematischen Problems betrachten wir die Lösung quadratischer Gleichungen der Form

\[x^2 + p x + q \, = \, 0\]

als Funktion \(x = f(d)\) der gegeben Daten \(d=(p,q) \in \R^2\). Nehmen wir die positive Wurzel im Fall \(p^2 > 4 q\), so lässt sich die Lösung \(x \in \R\) mit Hilfe der Mitternachtsformel wie folgt berechnen:

\[x \, = \, f(p,q) \, = \, - \frac{p}2 + \sqrt{\frac{p^2}4-q}.\]

Wir berechnen für den Verstärkungsfaktor zunächst die partiellen Ableitungen und erhalten die Jacobi-Matrix \(Df(p,q)\) als

\[\begin{aligned} Df(p,q) \, = \, \left(-\frac{1}2 + \frac{p}{2\sqrt{\frac{p^2}4-q}}, -\frac{1}{\sqrt{\frac{p^2}4-q}}\right). \end{aligned}\]

Damit lässt sich der Verstärkungsfaktor in (2.9) berechnen als

\[\begin{aligned} V \ = \ \frac{\left\Vert \left(-\frac{1}2 + \frac{p}{2\sqrt{\frac{p^2}4-q}}, -\frac{1}{\sqrt{\frac{p^2}4-q}}\right) \right\Vert \cdot \Vert (p,q) \Vert} {\Vert - \frac{p}2 + \sqrt{\frac{p^2}4-q} \Vert}. \end{aligned}\]

Wir sehen, dass wir typischerweise einen großen Verstärkungsfaktor erhalten, wenn der Fall \(q \rightarrow \frac{p^2}{4}\) auftritt, d.h. wenn wir nahe einer doppelten Nullstelle sind oder wenn der Fall \(q \rightarrow 0\) auftritt, d.h. wenn eine Nullstelle nahe Null ist.

2.5.2. Konvergenz numerischer Verfahren

Bisher haben wir nur das Verhalten des Problems, z.B. der exakten Lösung linearer Gleichungssysteme, unter Störungen der Daten betrachtet, jedoch nicht das Verhalten bei einem speziellen numerischen Verfahren mit Rundungsfehlern und Approximationsfehlern untersucht. Zu einem Problem \(x=f(d)\) mit \(f:\R^n\to\R^m\) betrachten wir also nun eine Folge von Funktionen

\[\begin{aligned} f_k:\R^n\to\R^m, k\in\N \end{aligned}\]

als sogenanntes numerisches Verfahren, welches die exakte Lösung \(f\) approximieren soll. Unter dieser Folge könnten wir z.B. eine Folge von Rundungsfehlern verstehen, die gegen Null konvergiert, oder aber ein Iterationsschema, das eine Lösung approximiert, wie im folgenden Beispiel des Heron-Verfahrens zur numerischen Berechnung der Wurzel.

Beispiel 2.14 (Heron-Verfahren)

Wir betrachten das mathematische Problem

\[\begin{aligned} f(d) :=\sqrt{d}, \end{aligned}\]

d.h. wir wollen die Wurzel für gegebene Daten für \(d\in\R^+_0\) berechnen. Das bereits in der Antike bekannte Heron-Verfahren zur Approximation der Wurzel ist durch folgende Iterationsvorschrift gegeben:

\[\begin{aligned} x_{k+1} \: = \: \frac{1}2 \left( x_k + \frac{d}{x_k} \right), \end{aligned}\]

mit gegebenem Anfangswert \(x_0\in\R^+\).

Somit haben wir also ein approximatives Verfahren gegeben durch:

\[\begin{aligned} f_{k+1}(d) \: \coloneqq \: x_{k+1} \: = \: \frac{1}2 \left( x_k + \frac{d}{x_k} \right). \end{aligned}\]

Für den Anfangswert kann beispielsweise \(x_0 \coloneqq 1\) verwendet werden oder eine leicht bessere Schätzung für die gesuchte Wurzel \(x_0 \coloneqq (d+1)/2\). In Abb. 2.8 visualisieren wir jeweils 10 Iteration für verschiedene Daten \(d \in \R^+_0\) und unterschiedliche Anfangswerte.

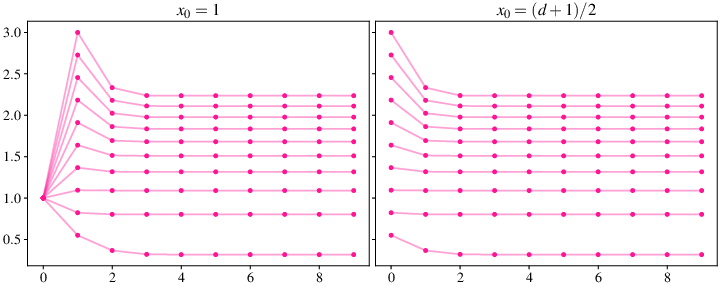
Abb. 2.8 Verhalten des Heron-Verfahrens aus Beispiel 2.14 für verschiedene \(d\in\R^+_0\) und unterschiedliche Anfangswerte.

Dieses Beispiel motiviert auch, dass wir im Folgenden immer \(D\subset \R^n\) als Menge der zulässigen Daten betrachten werden, d.h. wir wollen die zulässigen Daten in manchen Fällen einschränken.

Eine wichtige Eigenschaft für numerische Verfahren ist die sogenannte Konsistenz. Sie besagt im Wesentlichen, dass das Verfahren für ungestörte Daten auch wirklich gegen die echte Lösung des Problems konvergiert.

Definition 2.12 (Konsistenz eines numerischen Verfahrens)

Für ein gegebenes Lösungsverfahren \(f:D\to\R^m\) heißt ein numerisches Verfahren mit \(f_k:D\to\R^m\) konsistent zu \(f\), falls

\[\begin{aligned} \lim_{k\to\infty} f_k(d) \: = \: f(d) \end{aligned}\]

für alle \(d\in D\) gilt.

Wir können den Begriff der Konsistenz anhand des Heron-Verfahrens betrachten.

Beispiel 2.15 (Konsistenz des Heron-Verfahrens)

Wir zeigen zunächst, dass das Heron-Verfahren \(f_k \colon \R_0^+ \rightarrow \R_0^+\) konvergiert. Dazu sehen wir, dass für beliebige \(k\in\N^+\) gilt

\[\begin{aligned} x_{k+1}^2 \: &= \: \frac{1}{4}\left(x_k + \frac{d}{x_k}\right)^2 \: = \: \frac{1}{4}\left(x_k^2 + 2d + \frac{d^2}{x_k^2}\right)\\ \: &= \: \frac{1}{4}\left(x_k^2 - 2d + \frac{d^2}{x_k^2} + 4d\right) \: = \: \frac{1}{4}\left(\left(x_k - \frac{d}{x_k}\right)^2 + 4d\right) \: \geq \: d. \end{aligned}\]

Somit gilt also \(\abs{x_k}\geq \sqrt{d}\) für alle \(k\geq 1\). Da \(x_0> 0\) gilt zeigen wir mit Hilfe von vollständiger Induktion, dass \(x_k \geq \sqrt{d}\) für \(k\geq 1\) gilt. Jede Zwischenlösung \(x_k \in \R^+\) des Iterationsverfahrens ist in diesem Fall also von unten beschränkt.

Weiterhin folgt für \(k\geq 1\) dann, dass

\[\begin{aligned} x_{k+1} \: = \: \frac{1}{2} \left(x_k + \frac{d}{x_k}\right) \: \leq \: \frac{1}{2} \left(x_k + \frac{x_k^2}{x_k}\right) \: = \: x_k. \end{aligned}\]

Somit ist die Folge für \(k\geq 1\) monoton fallend und beschränkt nach unten und somit offensichtlich konvergent.

Sei nun \(x^\ast:=\lim_{k\to\infty} x_k\) der Grenzwert, dann erfüllt dieser die Fixpunktgleichung

\[\begin{aligned} x^\ast = \frac{1}{2} \left(x^\ast + \frac{d}{x^\ast}\right) \quad \Leftrightarrow \quad 2 (x^\ast)^2 = (x^\ast)^2 + d \quad \Leftrightarrow \quad (x^\ast)^2 = d, \end{aligned}\]

und somit löst \(x^\ast\) das Problem. Weiterhin gilt \(x^* = \lim_{k\to\infty} x_k \geq \sqrt{d}\) und somit gilt \(x^\ast = \sqrt{d}\).

Für den Fall \(x_0<0\) kann man analog zeigen, dass \((x_k)_{k \in \N}\) eine monoton steigende Folge ist, die durch \(x_k \leq -\sqrt{d}\) nach oben beschränkt ist. Hier gilt dann \(x^\ast = -\sqrt{d}\).

Aus den vorherigen Abschnitten, wissen wir bereits, dass es bei der Lösung von mathematischen Problemen relevant ist, das Lösungsverhalten bei Störungen in den Daten \(d\) zu betrachten. Für numerische Verfahren wollen wir bei Störungen sicherstellen, dass Konsistenz im Sinne von Definition 2.12 gegeben ist, sofern auch die Störung der Daten gegen null konvergiert. Dies führt auf die Definition der Konvergenz.

Definition 2.13 (Konvergenz eines numerischen Verfahrens)

Für \(f:D\to\R^m\), heißt das numerische Verfahren \(f_k:D\to\R^m\) konvergent zum Problem \(x=f(d)\), falls

\[\begin{aligned} \lim_{k\to\infty} f_k(d_k) = f(d) \end{aligned}\]

für alle Folgen von Daten \((d_k)_{k\in\N}\) mit \(\lim_{k\to\infty} d_k\to d\) gilt.

Beispiel 2.16 (Verrauschtes Heron-Verfahren)

Wir führen nun das Heron-Verfahren mit verrauschten Daten für \(d=2\) durch, d.h., in jedem Schritt haben wir

\[\begin{aligned} x_{k+1} \: = \: f_{k+1}(d_{k+1}) \: = \: \frac{1}{2} \left(x_k + \frac{d_{k+1}}{x_k}\right). \end{aligned}\]

Hierbei setzen wir die verrauschten Daten \(d_{k+1} \coloneqq d + \sigma_k\), wobei \(\sigma_k \sim \mathcal{N}(0,\delta_k)\) eine normalverteilte Größe mit Varianz \(\delta_k\) ist. Für unser Experiment wählen wir eine Nullfolge \(\delta_k\to 0\), so dass die Folge im Erwartungswert konvergiert, d.h. \(\mathds{E}(d_k) \to d\). fig:noisyHeron zeigt das Verfahren für unterschiedliche Durchläufe bei denen jeweils unterschiedliches zufällig gewähltes Rauschen auftritt. Man erkennt, dass das Verfahren in den meisten Fällen gegen \(\sqrt{d} = \sqrt{2}\) konvergiert.

Falls \(\sigma_k\) allerdings so groß wird, dass ein Folgeglied \(x_{k+1}\) negativ wird, konvergiert das Verfahren gegen \(-\sqrt{d} = -\sqrt{2}\).

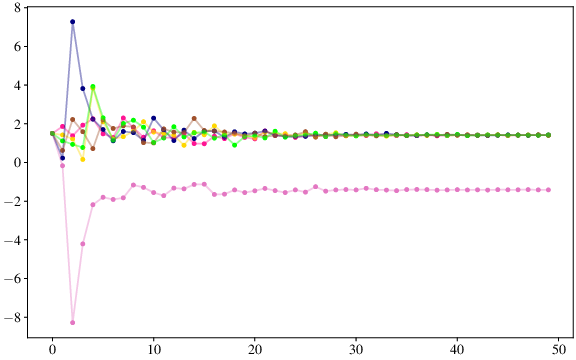
Abb. 2.9 Visualisierung des Heron-Verfahrens mit verrauschten Daten \(d_k\) aus Beispiel 2.16.

Konvergenz von numerischen Verfahren ist in vielen Fällen schwierig direkt zu beweisen. Wir können aber einen geschickten Zusatz über den Begriff der Stabilität wählen. Wir definieren Stabilität eines numerischen Verfahrens hierbei im Wesentlichen als gleichgradige Stetigkeit der Folgeglieder \(f_k\), welche besagt, dass wir die Auswirkung von Störungen auf den numerischen Algorithmus kontrollieren können. In diesem Sinne ist Stabilität verwandt mit dem Begriff der Kondition aus den letzten Abschnitten.

Definition 2.14 (Stabilität eines numerischen Verfahrens)

Ein numerisches Verfahren \(f_k:D\to\R^m, k\in\N\) heißt stabil, falls für jedes vorgegebene \(\epsilon>0\) ein \(\delta>0\) existiert, so dass für alle \(k\in\N\) gilt

\[\begin{aligned} \norm{\Delta_d} < \delta \quad \Rightarrow \quad \norm{f_k(d + \Delta_d) - f_k(d)} < \epsilon. \end{aligned}\]

Aus Definition 2.14 lässt sich für ein stabiles numerisches Verfahren direkt ableiten, dass für eine Folge von Daten \((d_k)_{k \in \N} \subset D\) mit immer kleiner werdenden Störungen, d.h., \(\lim_{k \rightarrow \infty} d_k = k\), gilt:

\[\begin{aligned} \lim_{k\to \infty} \norm{f_k(d_k) - f_k(d)} \, = \, 0. \end{aligned}\]

Eine einfachere Definition ist im Falle Lipschitz-stetiger Funktionen \(f_k\) möglich. In diesem Fall sprechen wir von Stabilität des numerischen Verfahrens wenn eine Konstante \(L > 0\) unabhängig von \(k \in \N\) existiert, so dass

\[\begin{aligned} \norm{f_k(d + \Delta_d) - f_k(d)} \ \leq \ L \cdot \norm{\Delta_d} \end{aligned}\]

für alle \(k\in\N\), alle zulässigen Daten \(d\in D\) und alle zulässigen Störungen \(\Delta_d \in D\) gilt. Stabilität bedeutet also im Wesentlichen, dass Fehler durch das Verfahren nicht zu sehr bzw. nicht unkontrolliert verstärkt werden können.

Eine grundlegende Erkenntnis in der Numerik ist, dass sich die Konvergenz eines numerischen Verfahrens aus dessen Konsistenz und Stabilität ergibt.

Satz 2.5 (Konvergenz eines Verfahrens)

Es sei \(f_k:D\to\R^m\) für \(k\in\N\) ein numerisches Verfahren zur Lösung eines mathematischen Problems. Dann gilt folgende (informelle) Implikation:

Proof. Die Aussage folgt direkt aus der Dreiecksungleichung. Sei dazu \(d\in D\) und \((d_k)_{k\in\N} \subset D\) eine Folge von Daten, so dass \(\lim_{k\to\infty} d_k = d\). Dann gilt

(2.10)\[\begin{split} \norm{f_k(d_k) - f(d)} \: &= \: \norm{f_k(d_k) - f_k(d) + f_k(d) - f(d)}\\ \: &\leq \: \underbrace{\norm{f_k(d_k) - f_k(d)}}_{\textbf{Stabilitäts-Term}} + \underbrace{\norm{f_k(d) - f(d)}}_{\textbf{Konsistenz-Term}}. \end{split}\]

Wegen der angenommenen Stabilität des numerischen Verfahrens wissen wir, dass

\[\begin{aligned} \lim_{k\to \infty} \norm{f_k(d_k) - f_k(d)} \, = \, 0. \end{aligned}\]

Analog, können wir aus der angenommenen Konsistenz des numerischen Verfahrens folgern, dass gilt

\[\begin{aligned} \lim_{k\to \infty} \norm{f_k(d) - f(d)} \, = \, 0. \end{aligned}\]

Hieraus können wir wegen der Abschätzung (2.10) direkt folgern, dass gilt

\[\begin{aligned} \lim_{k\to\infty} \norm{f_k(d_k) - f(d)} \, = \, 0, \end{aligned}\]

das heißt, dass numersiche Verfahren also konvergent ist. ◻

Ist ein numerisches Verfahren nicht stabil, so können wir im Allgemeinen auch keine Konvergenz erwarten. Im Folgenden wollen wir die Stabilität des Heron-Verfahrens untersuchen.

Beispiel 2.17 (Stabilität des Heron-Verfahrens)

Um die Stabilität des Heron-Verfahrens zu zeigen, wiederholen wir kurz dessen Definitiondes. Für \(d\in\R^+\) definieren wir das numerische Verfahren:

(2.11)\[\begin{aligned} f_{k+1}(d) \: \coloneqq \: \frac{1}{2}\left(f_k(d) + \frac{d}{f_k(d)} \right) \end{aligned}\]

mit gegebenem Startwert \(f_0(d) \in \R^+\). Die Auswertung von \(f_{k+1}\) an \(d\) ist also die \(k\)-te Iteration des Heron-Verfahrens, welche wiederum mit \(d\) durchgeführt wurde. So erhalten wir ein wohldefiniertes Verfahren und können \(f_k(d)\) mit \(f_k(d+\Delta_d)\) vergleichen für eine Störung \(\Delta_d \in \R\), so dass \(d + \Delta_d \in \R^+\) gilt.

Für die numerische Stabilität wollen wir zeigen, dass die Funktionen \(f_k\) Lipschitz-stetig sind und ein \(L>0\) unabhängig von \(k \in \N\) existiert, so dass gilt

\[\begin{aligned} \abs{f_{k+1}(d+\Delta_d) - f_{k+1}(d)} \: \leq \: L \cdot \abs{\Delta_d}. \end{aligned}\]

Dazu berechnen wir mit der Definition des Heron-Verfahrens in (2.11):

\[\begin{aligned} e_{k+1}:=f_{k+1}(d+\Delta_d) - f_{k+1}(d) \: &= \: \frac{1}{2}\left(f_k(d+\Delta_d) + \frac{d+\Delta_d}{f_k(d+\Delta_d)} - f_k(d) - \frac{d}{f_k(d)} \right)\\ % &= \: \frac{1}{2} \left( \bigl(f_k(d+\Delta_d) - f_k(d)\bigr) \cdot \left(1 - \frac{d + \Delta_d}{f_k(d+\Delta_d)\cdot f_k(d)}\right)\right)\\ &\quad - \frac{1}{2} \cdot \frac{d}{f_k(d)} + \frac{1}{2} \cdot \frac{d+\Delta_d}{f_k(d)}. \end{aligned}\]

Somit folgt also

\[\begin{aligned} \abs{e_{k+1}} \ \leq \ \frac{1}{2} \cdot \abs{e_k} \cdot \abs{1 - \frac{d+\Delta_d}{f_k(d+\Delta_d)\cdot f_k(d)}} + \frac{1}{2} \cdot \abs{\frac{\Delta_d}{f_k(d)}} \end{aligned}\]

Da für den Startwert \(f_0(d)>0\) gilt, wissen wir aus Beispiel 2.14, dass \(f_k(d)\geq \sqrt{d}\) für alle \(k \geq 1\) gilt und somit

\[\begin{aligned} \abs{\frac{\Delta_d}{f_k(d)}} \ \leq \ \frac{1}{\sqrt{d}} \cdot \abs{\Delta_d} \end{aligned}\]

Zusätzlich wollen wir, dass für ein \(q \in \R\) mit \(0 < q < 1\) gilt

\[\begin{aligned} \abs{1 - \frac{d+\Delta_d}{f_k(d+\Delta_d)\cdot f_k(d)}} \ < \ 2 q \end{aligned}\]

gilt, was gegeben ist, falls

\[\begin{aligned} \frac{d+\Delta_d}{f_k(d+\Delta_d)\cdot f_k(d)} \ < \ 2q + 1. \end{aligned}\]

Fordern wir nun, dass \(\abs{\Delta_d} < 2q d\) gilt, so folgt schon

\[\begin{aligned} \frac{d+\Delta_d}{f_k(d+\Delta_d)\cdot f_k(d)} \ \leq \ \frac{\sqrt{d+\Delta_d}}{\sqrt{d}} \ \leq \ \sqrt{2q + 1} \ \leq \ 2q + 1. \end{aligned}\]

Somit erhalten wir insgesamt mit Hilfe der geometrischen Reihe

\[\begin{aligned} \abs{e_{k+1}} \ &\leq \ q \abs{e_k} + \frac{1}{\sqrt{d}} \abs{\Delta_d} \ \leq \ \ldots \ \leq \ \frac{1}{\sqrt{d}} \abs{\Delta_d}\sum_{j=0}^{k} q^k \\ &\leq \ \frac{1}{\sqrt{d}} \abs{\Delta_d} \sum_{j=0}^{\infty} q^k \ = \ \frac{1}{(1-q)\sqrt{d}} \abs{\Delta_d}. \end{aligned}\]

Somit ist das Heron-Verfahren auf einer nach unten beschränkten Menge, \(D:= [a,\infty)\) mit \(a>0\) Lipschitz-stetig mit

\[\begin{aligned} \abs{f(d+ \Delta_d) - f(d)} \ \leq \ L \cdot \abs{\Delta_d}, \end{aligned}\]

wobei \(L \coloneqq \frac{1}{(1-q)\sqrt{a}}\) mit \(\abs{\Delta_d} < 2q a\). Damit ist das Heron-Verfahren numerisch stabil.