7.2. Der Satz von Gerschgorin

In vielen Fällen benötigt man zumindest grobe Abschätzungen über die Lage von Eigenwerten, etwa um den Spektralradius abzuschätzen oder ein vernünftiges \(\lambda\) für die inverse Iteration zu wählen. Ein zentrales Hilfsmittel sind die Gerschgorin-Kreise.

Definition 7.1 (Gerschgorin-Kreise)

Für eine Matrix \(A\in\C^{n\times n}\) sind die zeilenweisen Gerschgorin-Kreise für \(i=1,\ldots, n\) definiert durch

\[\begin{aligned} R_i := \{ \lambda \in \mathbb{C} ~|~ \abs{\lambda-A_{ii}}\leq \sum_{j \neq i} \vert a_{ij} \vert \}. \end{aligned}\]

Die spaltenweisen Gerschgorin-Kreise definiert man analog durch

\[\begin{aligned} S_i := \{ \lambda \in \mathbb{C} ~|~ \abs{\lambda-A_{ii}}\leq \sum_{j \neq i} \abs{A_{ji}}\}. \end{aligned}\]

Der Satz von Gerschgorin zeigt, dass alle Eigenwerte in diesen Kreisen liegen

Satz 7.1 (Satz von Gerschgorin)

Sei \(A \in \mathbb{C}^{n \times n}\) und die Gerschgorin Kreise definiert wie oben. Dann gilt für alle Eigenwerte \(\lambda\) von \(A\)

\[\begin{aligned} \lambda \in \left(\bigcup_{j=1}^n R_j \right) \cap \left(\bigcup_{j=1}^n S_j \right). \end{aligned}\]

Proof. Es genügt zu zeigen, dass \(\lambda \in \bigcup_{j=1}^n R_j\) gilt, denn da die Eigenwerte von \(A\) jenen von \(A^T\) entsprechen, folgt dann sofort auch \(\lambda \in \bigcup_{j=1}^n S_j\). Wir schreiben \(A = D+E\) mit \(D=\text{diag}(A_{11},\ldots, A_{nn})\) einer Diagonalmatrix \(E = A-D\) eine Matrix mit Nulldiagonale. Sei \(\lambda\) ein Eigenwert und \(v\) der zugehörige Eigenvektor, so folgt aus \(Av = \lambda v\) auch

\[\begin{aligned} (D - \lambda I)v = Dv - \lambda v = - Ev . \end{aligned}\]

Fall I.: Falls \(\lambda = A_{ii}\) für ein \(i\in\{1,\ldots,n\}\), dann gilt \(\lambda \in R_i\) und die Aussage ist gezeigt.
Fall II.: Andernfalls ist \(D-\lambda I\) invertierbar und somit

\[\begin{aligned} v = (\lambda I-D)^{-1}Ev, \end{aligned}\]

also

\[\begin{aligned} v_i = \sum_{j\neq i} \frac{A_{ij}}{\lambda - A_{ii}} v_j. \end{aligned}\]

Daraus folgt

\[\begin{gathered} \max_i \vert v_i \vert \leq \max_i \sum_{j\neq i} % \frac{\abs{A_{ij}}}{\vert \lambda - A_{ii}\vert} \vert v_j\vert \leq \max_i \sum_{j\neq i} \frac{\vert A_{ij}\vert }{\vert \lambda - A_{ii}\vert} \max_k \abs{v_k}\\ \Rightarrow 1\leq \max_i \sum_{j\neq i} \frac{\abs{A_{ij}}}{\vert \lambda - A_{ii}\vert} \end{gathered}\]

Es existiert also \(i\in\{1,\ldots,n\}\), s.d.

\[\begin{aligned} \abs{\lambda - A_{ii}} \leq \sum_{j\neq i} \abs{A_{ij}} \end{aligned}\]

. ◻

Der Satz von Gerschgorin liefert auch sofort ein interessantes Resultat über eine Klasse von Matrizen, die in der Numerik eine wichtige Rolle spielen.

Korollar 7.2

Sei \(A \in \mathbb{C}^{n \times n}\) strikt diagonaldominant, d.h.

\[\vert A_{ii}\vert > \sum_{j\neq i} \vert A_{ij}\vert\]

für alle \(i\). Dann liegt \(\lambda = 0\) in keinem Gerschgorin-Kreis, d.h. \(A\) ist invertierbar.

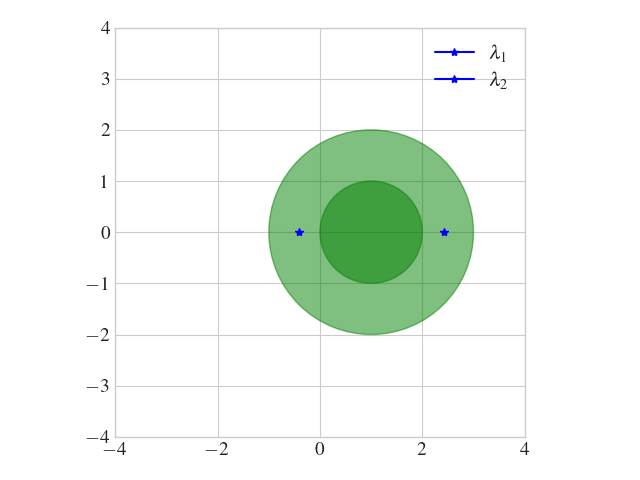
Abb. 7.3 Die Gerschgorin-Kreise für die Matrix aus Beispiel 7.3.