4.2. Das Newton-Verfahren

Bis jetzt haben wir allgemein diskutiert, wie sich Fixpunktiterationen für die Lösung von nichtlinearen Gleichungen nutzen lassen und wie man die Konvergenz dieser sicherstellt. Bisher haben wir jedoch die konkrete Konstruktion einer Fixpunktiteration nur für bestimmte Beispiele angegeben. Interessanter ist es natürlich allgemeine Verfahren kennen zu lernen, die sich für eine breite Klasse von mathematischen Problemen anwenden lassen. Als ein sehr prominentes Beispiel für ein solch allgemeines Verfahren betrachten wir das populäre Newton-Verfahren.

Die grundlegende Idee des Newton-Verfahrens ist es die nichtlineare Gleichung geeignet zu approximieren, so dass sich deren Lösung auf den bekannten Fall von linearen Gleichungssystemen zurückführen lässt. Nehmen wir im Folgenden an, dass die Funktion \(F \colon \R^n \rightarrow \R^n\) differenzierbar sei. Konkret linearisiert man dann die Gleichung \(F(x)=0\) um die aktuelle Iterierte mittels einer Taylor-Approximation 1. Ordnung, d.h.

\[F(x) \ \approx \ F(x_k) + F'(x_k) (x-x_k),\]

wobei wir mit \(F'(x_k)\) die Jacobi-Matrix der Funktion \(F\) bezeichnen.

Nun ist man wieder im Fall von linearen Gleichungssystemen und berechnet anstatt der gesuchten Nullstelle von \(F\) eine Lösung des linearen Gleichungssystems

\[Ax \ \coloneqq \ F'(x_k)x \ = \ F'(x_k)x_k - F(x_k) \ =: \ b.\]

Wir setzen nun die nächste Iterierte \(x_{k+1}\) als Lösung des linearen Gleichungssystems, so dass für die Approximation gilt

\[F(x_k) + F'(x_k) (x_{k+1}-x_k) \approx 0.\]

Nehmen wir nun an, dass die Jacobi-Matrix \(F'(x_k)\) regulär ist, so lässt sich das Newton-Verfahren als Iterationsverfahren angeben:

(4.3)\[x_{k+1} \ = \ x_k - (F'(x_k))^{-1} F(x_{k}).\]

Die Fixpunktfunktion \(G \colon \R^n \rightarrow \R^n\) des Newton-Verfahrens lässt sich also angeben als

\[G(x) \ \coloneqq \ x - (F'(x))^{-1} F(x).\]

Das folgende Beispiel illustriert das Newton-Verfahren im Eindimensionalen.

Beispiel 4.2 (Newton-Verfahren zur Wurzelberechnung)

Wir möchten analog zum Heron-Verfahren in Beispiel 2.14 die positive Quadratwurzel einer positiven reellen Zahl \(a \in \R^+\) berechnen, d.h. wir suchen die Zahl \(x \in \R^+\), so dass \(x^2 = a\) gilt. Zunächst stellen wir dieses mathematische Problem zu einem Nullstellenproblem für eine nichtlineare Funktion \(F \colon \R \rightarrow \R\) um:

\[F(x) \ \coloneqq \ 1 - \frac{a}{x^2} \ = \ 0.\]

Die Ableitung von \(F\) ist \(F'(x) = \frac{2a}{x^3}\) und existiert offensichtlich falls \(x \neq 0\).

Wir formulieren nun das Newton-Verfahren aus (4.3) in diesem eindimensionalen Beispiel als

\[x_{k+1} \ = \ x_k - \frac{F(x_{k})}{F'(x_k)} \ = \ x_k - \frac{1 - a/x_k^2}{2a / x_k^3} \ = \ \frac{3x_k}{2} - \frac{x_k^3}{2a}\]

Wählen wir nun beispielsweise die Zahl \(a=2\) und den Startwert \(x_0 = 1.5\) als Näherung der Quadratwurzel, so ergeben sich die folgenden Iterationen für das Newtonverfahren:

\[\begin{split} x_0 \ &= \ 1.5\\ x_1 \ &= \ 1.40\\ x_2 \ &= \ 1.414\\ x_3 \ &= \ 1.414213514\\ x_4 \ &= \ 1.41421356237309502\\ x_5 \ &= \ 1.414213562373095048801688724209697\\ \end{split}\]

Das Verfahren konvergiert offensichtlich sehr schnell gegen \(\sqrt{2}\). Wir werden später näher diskutieren warum dies so ist.

Das Newton-Verfahren lässt sich auch geometrisch anschaulich illustrieren, wie die folgende Bemerkung festhält.

Bemerkung 4.2

In einer Dimension lässt sich das Newton-Verfahren wie folgt veranschaulichen. Zunächst wird die nichtlineare Funktion \(F\) für die aktuelle Iteration \(x_k\) durch die Tangente an den Graphen \((x_k,F(x_k))\) approximiert. Anschließend wird die nächste Iterierte \(x_{k+1}\) aus dem Schnittpunkt dieser Tangente mit der \(x\)-Achse bestimmt. Abbildung Abb. 4.1 illustriert die geometrische Interpretation des Newton-Verfahren für eine eindimensionale Funktion.

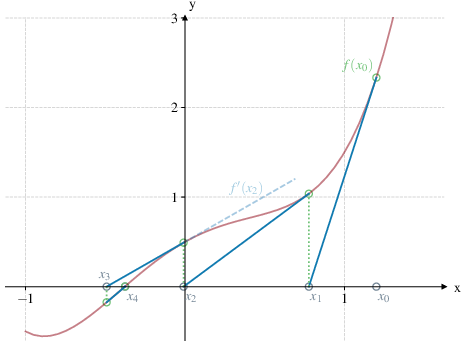
Abb. 4.1 Geometrische Illustration des Newton-Verfahrens im Eindimensionalen durch Annäherung mittels Tangenten.

4.2.1. Lokale Regularität der Jacobi-Matrix

Bisher haben wir angenommen, dass die Funktion \(F\) differenzierbar ist und die Jacobi-Matrix \(F'\) stets regulär ist. Tatsächlich ist das Newton-Verfahren nur sinnvoll definiert in einer Umgebung des Fixpunkts \(\overline{x}\) wenn \(F'(x)\) für alle Punkte \(x\) in dieser Umgebung tatsächlich regulär ist. Um dies zu garantieren hilft uns das folgende nützliche Resultat.

Lemma 4.1 (Lokale Regularität)

Sei \(F: \R^n \rightarrow \R^n\) eine Funktion, die in einer Umgebung des Fixpunkts \(\overline{x}\) stetig differenzierbar ist und sei außerdem \(F'(\overline{x})\) regulär. Dann existiert eine Umgebung \(B_\delta(\overline{x})\) des Fixpunkts \(\overline{x}\), so dass die Jacobi-Matrix \(F'(x)\) regulär ist für alle Punkte \(x \in B_\delta(\overline{x})\) in der Umgebung.

Proof. Wegen der Stetigkeit der Ableitung gibt es zu jedem \(\epsilon > 0\) ein \(\delta > 0\), so dass

\[\Vert F'(x) - F'(\overline{x}) \Vert \, < \, \epsilon, \qquad \forall~x \in B_\delta(\overline{x}).\]

Wir betrachten zunächst die folgende nützliche Identität:

(4.4)\[F'(x) \ = \ F'(\overline{x}) - (F'(\overline{x}) - F'(x)) ) \ = \ F'(\overline{x}) ( I_n - \underbrace{F'(\overline{x})^{-1}(F'(\overline{x}) - F'(x))}_{=: \: B}).\]

Sei nun konkret \(\epsilon < \frac{1}{\Vert F'(\overline{x})^{-1} \Vert}\) gewählt, dann existiert ein \(\delta > 0\), so dass für jedes \(x \in B_\delta(\overline{x})\) gilt:

\[\Vert B \Vert \ = \ \Vert F'(\overline{x})^{-1}(F'(\overline{x}) - F'(x)) \Vert \ \leq \ \underbrace{\Vert F'(\overline{x})^{-1} \Vert}_{< \, \epsilon^{-1}} \cdot \underbrace{\Vert F'(\overline{x}) - F'(x) \Vert}_{< \, \epsilon} \, < \, 1 .\]

Nach Satz 2.2 über die Neumannsche Reihe ist also \(I_n - B\) regulär und da \(F'(\overline{x})\) regulär nach Voraussetzung war ist das Produkt der beiden Matrizen auch wieder regulär. Somit folgt wegen der Identität (4.4), dass die Jacobimatrix \(F'(x)\) für jedes \(x \in B_\delta(\overline{x})\) in der lokalen Umgebung um den Fixpunkt \(\overline{x}\) regulär sein muss. ◻

4.2.2. Konvergenz

Für den Fall, dass die Jacobi-Matrix in der Nullstelle der nichtlinearen Funktion \(F \colon \R^n \rightarrow \R^n\) invertierbar ist, können wir nun die lokale Konvergenz des Newton-Verfahrens nachweisen.

Satz 4.2 (Lokale Konvergenz des Newton-Verfahrens)

Sei \(F: \R^n \rightarrow \R^n\) in einer Umgebung von \(\overline{x}\) stetig differenzierbar und \(\overline{x} \in \R^n\) eine Nullstelle von \(F\) mit \(F(\overline{x}) = 0\). Sei außerdem die Jacobi-Matrix \(F'\) lokal Lipschitz-stetig und \(F'(\overline{x})\) regulär in der Nullstelle.

Dann existiert eine lokale Umgebung \(B_R(\overline{x})\), so dass das Newton-Verfahren für jeden Startwert \(x_0 \in B_R(\overline{x})\) gegen die Nullstelle \(\overline{x}\) konvergiert, d.h. \(\lim_{k \rightarrow \infty} x_k = \overline{x}\).

Proof. Wir betrachten zunächst nur Umgebungen mit \(0 < R < \delta\), wobei \(\delta\) der Radius aus Lemma 4.1 ist. Mit dessen Aussage wissen wir, dass \(F'(x)\) in einer solchen Umgebung immer regulär für alle \(x \in B_R(\overline{x})\) ist.

Es reicht nun die lokale Kontraktivität der Fixpunktiteration des Newton-Verfahrens mit \(G(x) = x - F'(x)^{-1}F(x)\) nachzuweisen, damit wir den Banachschen Fixpunktsatz aus Satz 4.1 anwenden können. Es gilt nun für alle Punkte \(x,y \in B_R(\overline{x})\) die folgende Abschätzung

\[\begin{split} \Vert G(x) - G(y) \Vert \ &= \ \Vert x - y- F'(x)^{-1} F(x) + F'(y)^{-1} F(y) \Vert \\ &= \ \Vert F'(x)^{-1} (F(y) - F(x) - F'(x)(y-x)) + (F'(y)^{-1}-F'(x)^{-1}) F(y) \Vert \\ &\leq \ \Vert F'(x)^{-1} (F(y) - F(x) - F'(x)(y-x)) \Vert + \Vert (F'(y)^{-1}-F'(x)^{-1}) F(y) \Vert \\ &= \ \Vert F'(x)^{-1} (F(y) - F(x) - F'(x)(y-x)) \Vert \\ & \qquad \qquad + \Vert (F'(y)^{-1}-F'(x)^{-1}) (F(y)-F(\overline{x})) \Vert . \end{split}\]

Wegen der Stetigkeit von \(F'\) können wir zunächst wegen Lemma 4.1 den Radius \(R\) so klein wählen, dass \(\Vert F'(x)^{-1} \Vert\) beschränkt ist, z.B. durch \(\Vert 2 F'(\overline{x})^{-1} \Vert\). Da \(F\) stetig differenzierbar ist, gilt insbesondere

\[\frac{\Vert F'(x)^{-1} (F(y) - F(x) - F'(x)(y-x)) \Vert }{\Vert x- y\Vert} \ \rightarrow \ 0\]

für \(\Vert x-y\Vert \rightarrow 0\). Da \(\Vert x -y \Vert < 2 R\) gilt können wir also für jedes \(q\) einen hinreichend kleinen Radius \(R\)finden, so dass gilt

\[\Vert F'(x)^{-1} (F(y) - F(x) - F'(x)(y-x)) \Vert \ < \ \frac{q}2 \Vert x -y \Vert.\]

Weiter können wir folgende Abschätzung treffen:

\[\begin{aligned} \Vert (F'(y)^{-1}-F'(x)^{-1}) (F(y)-F(\overline{x})) \Vert \ &= \ \Vert F'(y)^{-1}( F'(x) -F'(y)) F'(x)^{-1} (F(y)-F(\overline{x})) \Vert \\ &\leq \ \Vert F'(y)^{-1} \Vert ~\Vert F'(x)^{-1} \Vert ~ \Vert F'(x) -F'(y)\Vert~ \Vert F(y)-F(\overline{x}) \Vert. \end{aligned}\]

Da eine stetig differenzierbare Funktion insbesondere auch Lipschitz-stetig ist und wir die lokale Lipschitz-Stetigkeit von \(F'\) gefordert haben, gilt in einer Umgebung \(B_R(\overline{x})\) des Fixpunktes \(\overline{x}\):

\[\Vert F'(x) -F'(y)\Vert \ \leq \ C \Vert x- y\Vert, \qquad \Vert F(y)-F(\overline{x}) \Vert \ \leq \ \Vert y -\overline{x} \Vert \ \leq \ C \cdot R.\]

Außerdem sind nach Satz 2.2 über die Neumannsche Reihe \(\Vert F'(x)^{-1} \Vert\) und \(\Vert F'(y)^{-1} \Vert\) lokal beschränkt. Ist \(R\) hinreichend klein, so erhalten wir insgesamt also

\[\Vert (F'(y)^{-1}-F'(x)^{-1}) (F(y)-F(\overline{x})) \Vert \ \leq \ \frac{q}2 \Vert x -y \Vert.\]

Damit haben wir insgesamt die Kontraktivität der Fixpunktfunktion \(G\) nachgewiesen und somit erhalten wir nach dem Banachschen Fixpunktsatz in Satz 4.1 die Konvergenz des Newton-Verfahrens. ◻

Wir sehen im Beweis, dass mit kleiner werdendem \(R\) ein beliebig kleines \(q > 0\) in der Kontraktivität erreicht werden kann. Je näher wir also an die Lösung herankommen, desto schneller wird das Verfahren konvergieren. Dies motiviert die Frage des nächsten Abschnitts, nämlich wie wir unterschiedliche Konvergenzgeschwindigkeiten definieren und analysieren können.