3. Über- und unterbestimmte lineare Gleichungssysteme

Nachdem wir uns in Direkte Lösung linearer Gleichungssysteme mit der numerischen Lösung eines linearen Gleichungssystems \(Ax=b\) mit \(A \in \mathbb{R}^{n\times n}\) und \(x,b \in \mathbb{R}^n\) beschäftigt haben, wollen wir im Folgenden einen allgemeineren Fall untersuchen. Wir interessieren uns für lineare Gleichungssysteme der Form

\[Ax \ = \ b, \quad \text{ für } \ A \in \mathbb{K}^{m\times n} \ \text{ und } \ x \in \mathbb{K}^n, b \in \mathbb{K}^m,\]

wobei \(\K\in \{\R, \C\}\) wahlweise den Körper der reellen oder der komplexen Zahlen bezeichnet. Wir unterscheiden zwei Fälle für \(m \not= n\).

Definition 3.1

Es sei \(A\in\K^{m\times n}\) eine Matrix und \(b\in\K^m\), dann heißt das Gleichungssystem

(3.1)\[\begin{aligned} Ax = b \end{aligned}\]

• überbestimmt, falls \(m>n\) gilt,

• unterbestimmt, falls \(n>m\) gilt.

Im Falle überbestimmter Systeme übersteigt die Anzahl der Gleichungen die der unbekannten Variablen. Wir haben also mehr Gleichungen als Variablen. Im Falle unterbestimmter Systeme übersteigt die Anzahl der unbekannten Variablen die der Gleichungen. Wir haben also weniger Gleichungen als Variablen.

Bemerkung 3.1

Im Allgemeinen sind sowohl unterbestimmte als auch überbestimmte lineare Gleichungssysteme in (3.1) nicht lösbar. Aus diesem Grund muss man sich andere Strategien und Kriterien überlegen, um sinnvolle Aussagen über den unbekannten Vektor \(x \in \mathbb{K}^n\) treffen zu können.

Der Fall eines überbestimmten Gleichungssystems ist äußerst relevant, da er in vielen Anwendungen auftritt, wie z.B. bei der Bildrekonstruktion in der Computertomographie wenn die Anzahl der gemessenen Röntgenstrahlen \(m\) die Anzahl der zu rekonstruierenden Pixel \(n\) übertrifft.

Beispiel 3.1 (Ausgleichsgerade für experimentelle Daten)

Eine Person bekommt die Aufgabe für \(N \in \N\) Zahlen mit je \(n_i\in\N\) Ziffern die Quersumme zu bilden. Wir messen jeweils Zeit \(t_i \in \N\) in Sekunden, die dieser Vorgang benötigt und erhalten folgende Daten:

Anzahl der Ziffern \(n_i\)	5	6	8	9	11	16	30	23
Benötigte Zeit \(t_i\) in Sekunden	2	7	4	18	12	22	89	32

In Abb. 3.1 werden die experimentellen Daten visualisiert. Wir erwarten einen Zusammenhang zwischen der Anzahl der Ziffern und der Berechnungszeit, welcher sich durch eine lineare Funktion

\[\begin{aligned} t = f(t) = p_1 n + p_0 \end{aligned}\]

modellieren lässt mit unbekannten Koeffizienten \(p_1,p_0\in\R\). Für jeden Zahl \(i=1,\ldots,N\) erhalten wir also die Gleichung

\[\begin{aligned} p_1 n_i + p_0 = t_i. \end{aligned}\]

Ausgedrückt als lineares Gleichungssystem in Matrixschreibweise ergibt dies

\[\begin{aligned} \underbrace{ \begin{pmatrix} n_1 &1\\ \vdots\\ n_N &1\\ \end{pmatrix}}_{:=A} % \begin{pmatrix} p_1\\ p_0 \end{pmatrix} % = % \underbrace{ \begin{pmatrix} t_1\\ \vdots\\ t_N\\ \end{pmatrix}}_{:=b}. % \end{aligned}\]

Wir erhalten also ein überbestimmtes Gleichungssystem.

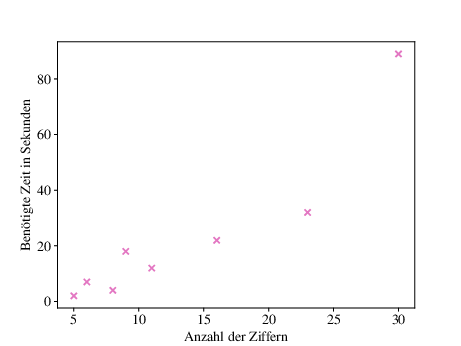
Abb. 3.1 Visualisierung der Daten in Beispiel 3.1.