3.2. QR-Zerlegung für überbestimmte Systeme

Wir haben oben die Lösung überbestimmter Systeme auf die Lösung der Normalengleichung zurückgeführt, die wir zum Beispiel mit der Cholesky-Zerlegung aus Cholesky-Verfahren lösen können. Dies ist aber nicht in allen Fällen der aus numerischer Sicht günstigste Weg um das Problem zu lösen.

Erstens kann sich die Kondition der Matrix des linearen Gleichungssystems stark erhöhen. Bei einer invertierbaren Matrix gilt nach Bemerkung 3.4 im Allgemeinen \(\kappa_2(A^T A) = \kappa_2(A)^2\). Zweitens kann der numerische Aufwand, der zum Aufstellen der Normalengleichung benötigt wird, sehr stark ansteigen. Die Berechnung des Matrixprodukts \(A^T A\) benötigt einen Aufwand in der Ordnung von \(\mathcal{O}(m\cdot n^2)\), während die anschließende Lösung mit Hilfe der Cholesky-Zerlegung in Algorithmus 1.5 nur einen Rechenaufwand der Ordnung \(\mathcal{O}(n^3)\) hat. Im stark überbestimmten Fall, d.h., für \(m>>n\), dominiert also der Aufwand zum Aufstellen der Normalengleichung gegenüber dem Aufwand für die eigentliche Lösung des linearen Gleichungssystems.

Beispiel 3.4 (Rechenaufwand der Normalengleichungen)

Wir wollen das lineare Ausgleichsproblem (3.2) mit Hilfe der Normalengleichungen lösen. Hierfür fixieren wir die Anzahl der Spalten als \(n=5\) und erzeugen zufällige Matrizen \(A\in\R^{m\times n}\) für \(m=2^i,i=1,\ldots, N\in\N\).

In Abb. 3.3 stellen wir links die Rechenzeit zur Lösung des Problems mit der Cholesky-Zerlegung dar. Der rot gefärbte Bereich stellt hierbei den Anteil zur Berechnung der Terme

\[\begin{aligned} A^T A,\quad A^Tb \end{aligned}\]

dar, der grüne den Anteil des Lösens mit Hilfe des Cholesky-Verfahrens. Wir erkennen, dass die Zeit um das Produkt zu berechnen den Gesamtrechenaufwand dominiert, der Aufwand für das Lösen des linearen Gleichungssystems mittels Cholesky-Verfahren bleibt wie erwartet konstant, da wir \(n=5\) fixieren.

Auf der rechten Seite, stellen wir die Variante dar, das Problem mithilfe der Singulärwertzerlegung von \(A\) wie in Lemma 3.2 zu lösen, was um Größenordnungen mehr Zeit benötigt. Hier dominiert allerdings die Zeit die Singulärwertzerlegung zu berechnen.

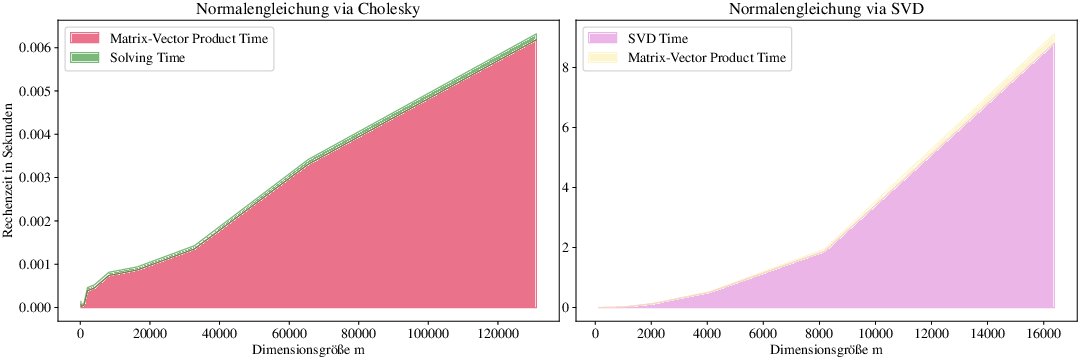
Abb. 3.3 Visualsierung für Beispiel 3.4.

3.2.1. Die QR-Zerlegung

Als Alternative betrachten wir analog zu Direkte Lösung linearer Gleichungssysteme wieder Zerlegungsmethoden zur direkten Lösung des Problems. Im Prinzip könnten wir versuchen genauso wie bei der LR-Zerlegung vorzugehen, allerdings ist unklar welche Art von Lösung wir damit berechnen würden. Insbesondere ist nicht zu erwarten, dass wir die gewünschte Kleinste-Quadrate-Lösung berechnen. Wir erkennen vor allem das folgende Problem durch die Anwendung von Elementarmatrizen zum Löschen von Spalten.

Im Allgemeinen gilt also für die Anwendung einer Elementarmatrix \(L_j\):

\[\begin{aligned} \norm{L_j(b- Ax)} \ &\neq \ \norm{b - Ax},\\ A^T L^T L A \ &\neq \ A^T A. \end{aligned}\]

Wir verlieren somit also die Kontrolle über das Residuum und auch die Normalengleichung.

Es kommt uns bei genauerer Betrachtung in den Sinn, dass hier eine Transformation mit orthogonalen Matrizen \(Q \in \R^{m \times m}\) besser geeignet ist, da diese das Residuum und die Normalengleichung nicht verändern, das heißt es gilt:

\[\begin{aligned} \norm{Q(b- Ax)} \ &= \ \norm{b-Ax},\\ A^T Q^T Q A \ &= \ A^T A. \end{aligned}\]

Definition 3.5 (QR-Zerlegung)

Für eine Matrix \(A\in\R^{m\times n}\) mit \(m\geq n\) nennt man eine Zerlegung der Form

\[\begin{aligned} A \: = \: Q \cdot R, \end{aligned}\]

mit einer orthogonalen Matrix \(Q\in\R^{m\times m}\) und einer rechten oberen Dreiecksmatrix \(R\in\R^{m\times n}\) eine QR-Zerlegung von \(A\).

Bemerkung 3.5 (Reduzierte QR-Zerlegung)

Die obere Dreiecksmatrix \(R\in \R^{m\times n}\) ist hierbei von der Form

\[\begin{aligned} R \: = \: \begin{pmatrix} R^{(1)}\\ 0 \end{pmatrix}, \end{aligned}\]

wobei \(R^{(1)}\in\R^{n\times n}\) eine quadratische, rechte obere Dreiecksmatrix ist und \(0\in\R^{(m-n)\times n}\) eine Nullmatrix ist, welche die Dimensionen entsprechend auffüllt. Wenn wir \(Q\) in die ersten \(n\) Spalten \(Q^{(1)}\in\R^{m\times n}\) und die letzten \((m-n)\) Spalten \(Q^{(2)}\in\R^{(m-n)\times n}\) aufteilen, so dass \(Q= (Q^{(1)} | Q^{(2)})\) gilt, so sehen wir, dass wir folgenden Zusammenhang erhalten:

\[\begin{aligned} Q R \ = \ (Q^{(1)}| Q^{(2)}) \begin{pmatrix} R^{(1)}\\ 0 \end{pmatrix} \ = \ Q^{(1)} R^{(1)} \end{aligned}\]

Somit reicht es, \(Q^{(1)}\) und \(R^{(1)}\) zu berechnen, was als sogenannte reduzierte QR-Zerlegung bekannt ist.

Haben wir nun eine QR-Zerlegung gegeben, so sehen wir, dass

\[\begin{aligned} \norm{b-Ax}^2 \ &= \ \norm{Q^T(b - Ax)}^2 \ = \ \norm{Q^Tb - Rx}^2 \\ &= \ \left\Vert \begin{pmatrix} (Q^{(1)})^T b \\ (Q^{(2)})^T b \end{pmatrix} - \begin{pmatrix} R^{(1)}x \\ 0\end{pmatrix} \right\Vert \ = \ \norm{(Q^{(1)})^T b - R^{(1)} x}^2 + \norm{Q^{(2)} b}^2.\\ %\norm{Q^Tb - Rx}^2 \ = \ \norm{(Q^{(1)})^T b^{(1)} - R^{(1)} x}^2 + \norm{Q^{(2)} b^{(2)}}^2, \end{aligned}\]

Wir sehen also, dass das Residuum für den Lösungsvektor

\[\begin{aligned} %\hat{x} \: = \: \left(R^{(1)}\right)^{-1} (Q^{(1)})^T b^{(1)} \hat{x} \: = \: \left(R^{(1)}\right)^{-1} (Q^{(1)})^T b \end{aligned}\]

minimiert wird. Diese Berechnung können wir analog zur LR-Zerlegung über Rückwärtseinsetzen in Algorithmus 1.1 lösen.

3.2.2. QR-Zerlegung mit Reflexionen und Rotationen

Nachdem wir bereits die gewünschten Eigenschaften einer QR-Zerlegung diskutiert haben, benötigen wir nun ein ein konkretes Verfahren, welches uns solch eine Zerlegung liefert.

Die Idee des QR-Verfahrens ist es eine Folge von orthogonalen Matrizen \(Q_1,\ldots,Q_n \in \R^{m \times m}\) zu konstruieren, so dass

\[\begin{aligned} R \: = \: Q_n \cdot \ldots \cdot Q_1 \cdot A \end{aligned}\]

eine rechte obere Dreiecksmatrix ist. Um die Matrizen \(Q_j \in \R^{m \times m}\) zu konstruieren, welche sukzessiv die Matrix \(A\) in eine obere rechte Dreiecksmatrix überführen, haben wir im wesentlichen zwei Möglichkeiten, nämlich:

1. eine Drehung (genannt: Givens-Rotation)

2. eine Spiegelung (genannt: Householder-Reflexion)

Im Zuge dieser Vorlesung werden wir uns ausschließlich mit Householder-Matrizen beschäftigen zur Berechnung der QR-Zerlegung. Für eine alternative Variante mittels Givens-Rotationen verweisen wir auf .

Definition 3.6 (Householder-Reflexion)

Für einen beliebigen, normierten Vektor \(v\in\R^{k}\) mit \(\norm{v}_2 = 1\) definieren wir die zugehörige Householder Matrix \(Q_v \in \R^{k \times k}\) als

\[\begin{aligned} Q_v \: \coloneqq \: I - 2 v v^T. \end{aligned}\]

Man beachte, dass es sich bei dem Term \(2vv^T\) um ein dyadisches Produkt handelt, welches zu einer Matrix von Rang \(1\) führt. Für Householder Matrizen gelten daher die folgenden nützlichen Eigenschaften.

Korollar 3.2 (Eigenschaften von Householder Matrizen)

Für einen beliebigen, normierten Vektor \(v\in\R^{k}\) mit \(\norm{v}_2=1\) ist die Householder Matrix \(Q_v\in\R^{k\times k}\) symmetrisch, orthogonal und selbstinvers.

Proof. Siehe Hausaufgabe. ◻

Beispiel 3.5 (Householder Matrix)

Wir berechnen für einen Vektor

\[v \: \coloneqq \: \frac{1}{5} \cdot \begin{pmatrix}3\\4\end{pmatrix}\]

die entsprechende Householder Matrix \(Q_v \in \R^{2 \times 2}\) als

\[\begin{aligned} Q_v \: = \: \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} -\frac{2}{25} \cdot \begin{pmatrix} 3\\4 \end{pmatrix} \cdot (3,4) \: = \: \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix} -\frac{2}{25} \cdot \begin{pmatrix} 9 & 12\\12 & 16 \end{pmatrix} \: = \: \begin{pmatrix} 0.28& -0.96\\ -0.96&-0.28 \end{pmatrix}. \end{aligned}\]

In Abb. 3.4 visualisieren wir den Effekt der Householder Matrix \(Q_v\) angewendet auf einen Vektor \(a \in \R^2\). Wir erkennen, dass \(Q_v a\) gerade die Spiegelung des Vektors \(a\) an der Hyperebene ist, die durch \(v \in \R^2\) als Normalenvektor induziert wird.

Abb. 3.4 Visualisierung einer Spiegelung mittels Householder-Matrix in Beispiel 3.5.

Das Ziel der Anwendung von Householder Matrizen \(Q_j \in \R^{m \times m}\) ist es immer Nullen unterhalb der Diagonalen von \(A\) zu erzeugen. Das bedeutet im konkreten Fall von \(Q_1\), dass wir die erste Spalte \(a_1 \in \R^m\) der Matrix \(A=(a_1|\ldots|a_n)\) auf ein Vielfaches des ersten Einheitsvektors \(e_1 \in \R^m\) spiegeln wollen. Es soll also für ein \(\lambda \in \R\) gelten:

\[\begin{aligned} Q_1 a_1 \: = \: \lambda e_1. \end{aligned}\]

In Beispiel 3.5 und Abb. 3.4 sehen wir, dass die Householder-Matrix \(Q\) eine Spiegelung an der Hyperebene mit Normalenvektor \(v\) realisiert. Wir wollen nun also einen Vektor \(v\in\R^{m}\) bestimmen, so dass der Vektor \(a_1\in\R^{m}\) gerade auf \(e_1 \in \R^m\) gespiegelt wird. Da sich die Länge des Vektors (und somit seine Euklidische Norm) bei einer Spiegelung nicht verändern kann, fordern wir also, dass gilt

\[\begin{aligned} Q_1 a_1 \: &= \: a_1 - 2 \langle v_1, a_1 \rangle v_1 \: = \: \norm{a_1} e_1\\ \Rightarrow \qquad v_1 \: &= \: \underbrace{\frac{-1}{2 \langle v_1, a_1 \rangle}}_{=: \,\mu} \cdot (a_1 - \norm{a_1} e_1). \end{aligned}\]

Da wir aber zusätzlich fordern, dass \(\norm{v_1} = 1\) gilt, folgt:

\[\begin{aligned} v_1 \: = \: \frac{\mu(a_1 - \norm{a_1} e_1)}{\norm{\mu(a_1 - \norm{a_1} e_1})} \: = \: \frac{\mu}{|\mu|} \cdot \frac{a_1 - \norm{a_1} e_1}{\norm{a_1 - \norm{a_1} e_1}} \: = \: \pm \, \frac{a_1 - \norm{a_1} e_1}{\norm{a_1 - \norm{a_1} e_1}} \end{aligned}\]

für \(a_1 \neq \lambda e_1, \lambda\in\R\). Falls \(a_1\) schon ein Vielfaches von \(e_1\) ist, brauchen wir in diesem Schritt keine Transformation und setzen \(v_1 =0\), was dazu führt, dass die Householder Matrix in diesem Fall einfach \(Q_1 = I_m\) ist.

Durch die Anwendung von \(Q_1\) auf \(A\) erhalten wir somit:

\[\begin{aligned} Q_1 \cdot A \ = \ \underbrace{% \begin{pNiceMatrix}[margin] R_{1,1} & R_{1,2} &\ldots & R_{1,n}\\ 0& \Block[fill=blue!15]{3-3}{\tilde{A}_1}\\ \vdots & & & \\ 0& & & \end{pNiceMatrix}}_{=: \, A_1} \end{aligned}\]

Wir haben also die erste Spalte von \(A\) erfolgreich auf den Einheitsvektor gespiegelt ohne die Matrixnorm von \(A\) zu verändern.

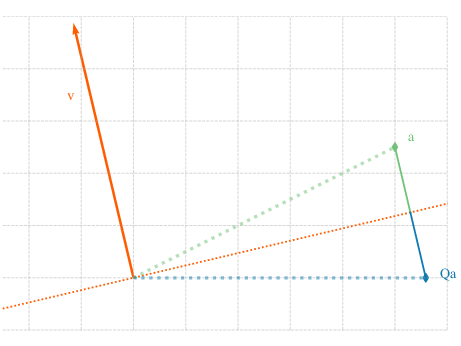
Abb. 3.5 Visualisierung einer Spiegelung des Vektors \(a\) auf \(e_1\).

Im zweiten Schritt reicht es die Untermatrix \(\tilde{A}_1\in\R^{(m-1)\times (m-1)}\) zu betrachten. Hierbei wählen wir nun die Spalte \(\tilde{a}_2\in\R^{m-1}\), welche wir auf den Einheitsvektor \(e_1^{(m-1)}\in\R^{m-1}\) spiegeln wollen. Analog zum ersten Schritt berechnen wir wieder die möglichen Normalenvektoren \(v_2 \in \R^{m-1}\) als

\[\begin{aligned} \tilde v_2 \: = \: \frac{\tilde a_2^1-\norm{\tilde a_2^1} e_1^{(m-1)}}{\norm{\tilde a_2^1-\norm{\tilde a_2^1}e_1^{(m-1)}}}. \end{aligned}\]

Somit können wir die entsprechende Householder Matrix \(\tilde{Q}_2 \in \R^{(m-1) \times (m-1)}\) berechnen als:

\[\tilde{Q}_2 \: = \: I - 2 \tilde v_2 \tilde v_2^T.\]

Die entsprechende Householder Matrix \(Q_2 \in \R^{m \times m}\), die die erste Zeile und Spalte von \(A\) bei Anwendung unverändert lässt, ist dementsprechend von der Form:

\[\begin{aligned} Q_2 \: \coloneqq \ : \begin{pmatrix} 1 & {0} \\ { 0} & \tilde {Q}_2 \end{pmatrix} \: = \: I - 2 v_2 v_2^T, \qquad v_2 \: = \: \begin{pmatrix} 0\\ \tilde v_2 \end{pmatrix}. \end{aligned}\]

Insgesamt erhalten wir nach der Anwendung von zwei Householder Matrizen per Konstruktion

\[\begin{aligned} Q_2\cdot (Q_1 \cdot A) \ = \ Q_2\cdot &\begin{pNiceMatrix}[margin] R_{1,1} & R_{1,2} &\ldots & R_{1,n}\\ 0& \Block[fill=blue!15]{3-3}{\tilde{A}_1}\\ \vdots & & & \\ 0& & & \end{pNiceMatrix} \ = \ \begin{pNiceMatrix}[margin] R_{1,1} & R_{1,2} &\ldots & R_{1,n}\\ 0& \Block[fill=blue!15]{3-3}{\tilde{Q}_2 \cdot \tilde{A}_1}\\ \vdots & & & \\ 0& & & \end{pNiceMatrix}\\ \ = \ &\begin{pNiceMatrix}[margin] R_{1,1} & R_{1,2} &\ldots & R_{1,n}\\ 0 & R_{2,2} &\ldots & R_{2,n}\\ \vdots & 0 &\Block[fill=green!15]{3-2}{\tilde{A}_2}\\ \vdots& \vdots & &\\ 0& 0 & & \end{pNiceMatrix}. \end{aligned}\]

Für die weiteren Schritte gehen wir analog vor und erhalten somit folgenden Algorithmus.

Algorithmus 3.1 (Householder QR-Verfahren)

function (Q, R) = qr(A):
    Q = I_m  # Initialisiere Matrix Q
    R = A  # Initialisiere Matrix R

    for j=0,...,n-1:
        v = R[j:m,j]  # Spalte unter j-tem Diagonalelement
        v[0] = v[0] - ||v||  # Konstruiere Spiegelvektor
        v  = v / ||v||  # Normalisierung
        Q_j = I_(m-j) - 2 * v * v^T # Konstruiere Spiegelmatrix
        R[j:m, j:n] = Q_j * R[j:m, j:n] # Spiegele auf Einheitsvektor
        Q[j:m, :] = Q_j * Q[j:m, :]  # Aktualisiere Q

Q = Q^T

Wir sehen direkt, dass uns dieses Verfahren tatsächlich eine QR-Zerlegung liefert.

Korollar 3.3 (QR-Verfahren)

Für eine Matrix \(A\in\R^{m\times n}\) liefert das QR-Verfahren in Algorithmus 3.1 eine QR-Zerlegung,

\[\begin{aligned} A \: = \: Q \cdot R, \end{aligned}\]

wobei insgesamt

• \(2m\cdot n^2 - 4/3 n^3\) FLOPS benötigt werden, falls nur die obere rechte Dreiecksmatrix \(R \in \R^{m \times n}\) berechnet wird,

• \(4(m^2\cdot n+n^3/3-m\cdot n^2)\) FLOPS benötigt werden, falls auch die orthogonale Matrix \(Q \in \R^{m \times m}\) berechnet wird.

Proof. Siehe Hausaufgabe. ◻

Im folgenden Beispiel wollen wir die QR-Zerlegung zur Lösung des linearen Ausgleichproblems nutzen und mit dem Cholesky-Verfahren vergleichen.

Beispiel 3.6 (QR-Zerlegung für das lineare Ausgleichsproblem)

Um den numerischen Rechenaufwand des QR-Verfahrens zu untersuchen, fixieren wir eine Matrix \(A\in\R^{m\times n}\) für \(m=2^{16}\) und \(n=5\) und erzeugen jeweils \(k\in \N\) zufällige Vektoren \(b \in \R^{m}\) für welche wir das lineare Ausgleichsproblem (3.2) lösen wollen.

Hierzu betrachten wir außerdem die entsprechenden Normalengleichungen der Form

\[\begin{aligned} A^T A x \: = \: A^T b. \end{aligned}\]

Da die Matrix \(A\) fixiert ist können wir für das Cholesky-Verfahren einmalig das Produkt \(A^TA\) berechnen, was insgesamt \(mn^2\) FLOPS benötigt. Zusammen mit dem Rechenaufwand der Cholesky-Zerlegung benötigen wir hier also \(\mathbf{m n^2 + 1/6 n^3 }\) FLOPS. Hier kommen noch weitere \(m \cdot n\) FLOPS hinzu für die Berechnung des Produkts \(A^T b\) und ein weiterer Rechenaufwand von \(\mathcal{O}(n^2)\) für die eigentliche Lösung des Systems mittels Rückwärtseinsetzen.

Für die Lösung mit Hilfe der QR-Zerlegung benötigen wir zunächst \(\mathbf{2mn^2 - 4/3 n^3}\) FLOPS um die QR-Zerlegung zu berechnen, \(m\cdot n\) FLOPS für die Berechnung von \((Q^{(1)})^T b^{(1)}\) und nochmal \(\mathcal{O}(n^2)\) Rechenoperationen für das Lösen des eigentlichen Systems via Rückwärtseinsetzen.

Eigentlich müsste der Rechenaufwand der QR-Zerlegung in vielen Fällen numerisch günstiger sein als das Cholesky-Verfahren. In der Praxis verwendet man allerdings sehr effiziente (und teilweise parallelisierte) Algorithmen zur Berechnung der Matrixmultiplikation \(A^TA\), deren benötigte Zeit niedriger ist der theoretischen Rechenaufwand \(m\cdot n^2\). Bei der QR-Zerlegung liefern diese Algorithmen weniger Vorteile, weshalb die QR-Zerlegung schlechter abschneidet beim Vergleich der Laufzeiten in Abb. 3.6.

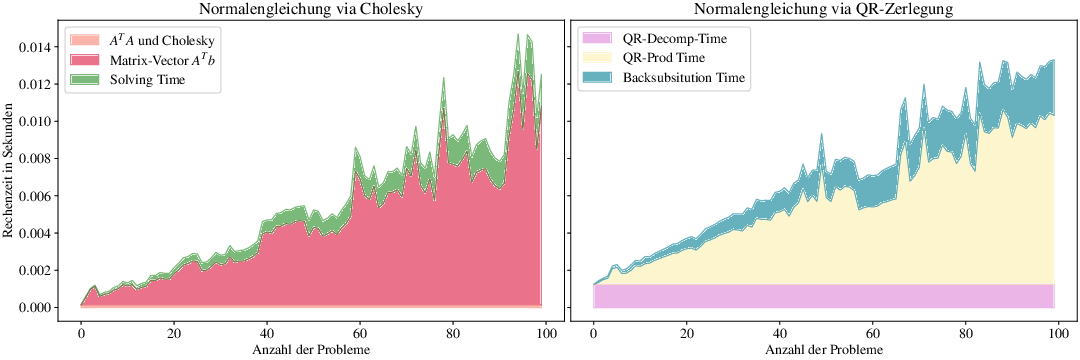
Abb. 3.6 Visualisierung für den Rechenaufwand zur Lösung des linearen Ausgleichsproblems mittels Cholesky-Verfahren und der QR-Zerlegung in Beispiel 3.6.