3.1. Gaußsche Normalengleichungen und Ausgleichsprobleme

In diesem Abschnitt beschäftigen wir uns mit Lösungsbegriffen, welche es uns erlauben überbestimmte Gleichungssystem, d.h., Probleme der Form (3.1) für \(m>n\), zu lösen.

3.1.1. Lineare Ausgleichsprobleme

Da eine exakte Lösung eines überbestimmten linearen Gleichungssystems in der Regel nicht möglich ist, versucht man die Abweichung von der idealen Lösung bezüglich einer Vektornorm zu minimieren. Typischerweise wählt man die Euklidische Norm, so dass man anstatt für das ursprüngliche Problem (3.1) für \(m > n\) nun ein Problem der folgenden Form hat, welches man auch lineares Ausgleichsproblem nennt.

Definition 3.2 (Lineares Ausgleichsproblem)

Es sei \(A\in\K^{m\times n}\) eine Matrix und \(b\in\K^m\) ein Vektor. Dann heißt das Minimierungsproblem

(3.2)\[\begin{aligned} \min_{x \in \mathbb{K}^n} ||b - Ax||_2 \end{aligned}\]

lineares Ausgleichsproblem.

Eine Lösung \(x\in\K^n\) nennt man Kleinste-Quadrate-Lösung oder auch im Englischen Least squares solution.

Wir wollen im folgenden Beispiel die Werte des linearen Ausgleichsproblems für die experimentellen Daten aus Beispiel 3.1 betrachten.

Beispiel 3.2 (Niveaumengen des linearen Ausgleichproblems)

Wir betrachten Lineare Ausgleichsproblem aus Beispiel 3.1 für \(A\in\R^{N \times 2}, b\in\R^N\). In Abb. 3.2 visualisieren wir zunächst die Funktion \(p\mapsto \norm{A p -b}\) über \(\R^2\). Wir erkennen, dass die Funktion konvex ist mit elliptischen Niveaulinien.

Zusätzlich markieren wir drei Punkte \(p^1, p^2, p^3 \in \R^2\), welche auf dem rechten Plot in ihrer Entsprechung als Geraden \(n\mapsto (p^i)_1 x + (p^i)_0\) für \(i=1,2,3\) visualisiert sind. Der pink gefärbte Punkt \(\hat{p} \in \R^2\) bzw. die pink gefärbte Gerade stellt hierbei die Lösung des linearen Ausgleichproblems (3.2) dar mit

\[\begin{aligned} \hat{p} \: \approx \: \begin{pmatrix} 2.9\\ -16.3 \end{pmatrix}. \end{aligned}\]

Die vertikalen Linien im Plot visualisieren jeweils die Fehler zu den Daten, welche quadriert addiert werden.

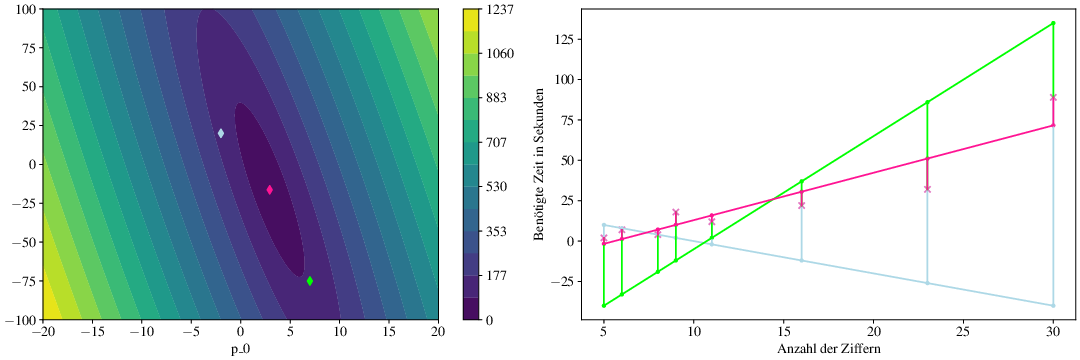
Abb. 3.2 Visualisierung des Ausgleichsproblems für ex:polyfit,ex:lstsqpoly.

Wir wollen uns im Folgenden mit numerischen Verfahren zur Berechnung von Kleinste-Quadrate-Lösungen und deren Eigenschaften beschäftigen.

3.1.2. Gaußsche Normalengleichung

Wir untersuchen zunächst die Eigenschaften einer Matrix, welche von links mit ihrer adjungierten Matrix multipliziert wurde, siehe Cholesky-Verfahren. Hierbei verwenden wir im Folgenden die Begriffe des Bildes und Kerns einer Matrix.

Definition 3.3 (Bild und Kern einer Matrix)

Sei \(A\in\K^{m\times n}\) eine Matrix. Der Kern der Matrix ist gegeben durch

\[\begin{aligned} \Kern(A) \ := \ \left\{x\in\K^n \, : \, Ax = 0 \right\}. \end{aligned}\]

Das Bild der Matrix ist definiert als

\[\begin{aligned} \Image(A) \ := \ \{y \in \K^m \, : \, \exists x\in\K^n \text{ mit } Ax = y \}. \end{aligned}\]

Darüber hinaus benötigen wir den Begriff des orthogonalen Komplements eines Unterraums.

Definition 3.4 (Orthogonales Komplement)

Sei \(U\subset\K^n\) ein Unterraum eines endlich-dimensionalen \(\K\)-Vektorraums. Wir definieren das orthogonale Komplement \(U^\perp\) von \(U\) bezüglich \(\K^n\) als

\[\begin{aligned} U^\perp := \{z\in\K^n: \langle u, z\rangle = 0,\quad \forall u\in U \}, \end{aligned}\]

wenn außerdem gilt:

\[\begin{aligned} \K^n = U \oplus U^\perp. \end{aligned}\]

Das heißt wir fordern

\[\K^n \: = \: U + U^\perp \quad \text{ und } \quad U \cap U^\perp \: = \: \{0\}.\]

Aus der linearen Algebra wissen, wir, dass ein auf \(U\) orthogonal stehender Untervektorraum \(V\) genau dann der Komplementärraum \(V=U^\perp\) bezüglich \(\K^n\) ist, falls gilt:

\[\begin{aligned} n \: = \: \dims (U) + \dims (V) \end{aligned}\]

Nun wollen wir uns wichtige Eigenschaften des Matrixprodukts herleiten, die gelten wenn man eine Matrix von links mit ihrer Adjungierten multipliziert.

Lemma 3.1 (Eigenschaften des Matrixprodukts mit der Adjungierten)

Es sei \(A\in\K^{m\times n}\) eine Matrix. Dann gilt

1. \(A^*A\in\K^{n\times n}\) ist hermitesch und positiv semi-definit,

2. die Matrix \(A^*A\) ist genau dann positiv definit, falls der Kern von \(A\) trivial ist, d.h., falls \(\mathcal{N}(A) = \lbrace 0 \rbrace\) gilt,

3. für den Kern und das Bild gelten die folgenden Identitäten

   \[\mathcal{N}(A^*A) \ = \ \mathcal{N}(A) \quad \ \text{ und } \ \quad \mathcal{R}(A^*A) \ = \ \mathcal{R}(A^*) \ = \ \mathcal{N}(A)^\perp.\]

Proof.  
Ad (i).
Die Hermizität der Matrix \(A^*A\) folgt offensichtlich aus der Kommutativität der komponentenweisen Multiplikation im Körper \(\K\). Ferner gilt für alle \(x \in \K^n\):

(3.3)\[\langle x, A^*Ax \rangle \ = \ x^*A^*Ax \ = \ (Ax)^*Ax \ = \ \langle Ax, Ax \rangle \ = \ \norm{Ax}_2^2 \ \geq \ 0.\]

Also ist \(A^*A\) immer positiv semi-definit.
Ad (ii).
Da offensichtlich gilt

\[\begin{aligned} \norm{Ax}_2^2 \, > \, 0 \ \text{ für } \ x\neq 0 \quad \Leftrightarrow \quad \Kern(A) = \{0\} \end{aligned}\]

sehen wir mit (3.3), dass

\[\begin{aligned} A^*A \text{ ist positiv definit} \quad \Leftrightarrow \quad \Kern(A) = \{0\}. \end{aligned}\]

Ad (iii).
Aus (3.3) folgt bereits, dass \(\mathcal{N}(A^*A) \subset \mathcal{N}(A)\) gilt. Die umgekehrte Inklusion \(\mathcal{N}(A) \subset \mathcal{N}(A^*A)\) gilt trivialerweise, da für ein beliebiges \(x\in \mathcal{N}(A)\)

\[(A^*A)x \ = \ A^*\underbrace{(Ax)}_{=0} \ = \ 0.\]

Somit haben wir also \(\mathcal{N}(A^*A) = \mathcal{N}(A)\) bewiesen.
Wir zeigen nun, dass \(\Image(A^*)\) und \(\mathcal{N}(A)\) orthogonal aufeinander stehen. Seien also \(z \in \Image(A^*)\) und \(x \in \mathcal{N}(A)\) beliebig. Dann gibt es ein \(y\in \mathbb{K}^m\), so dass \(z = A^*y\) gilt und damit

\[\langle x, z \rangle \ = \ x^*z \ = \ x^* A^*y \ = \ (Ax)^*y \ = \ 0^*y \ = \ 0.\]

Da dies für beliebige Vektoren \(z \in \mathcal{R}(A^*)\) und \(x \in \mathcal{N}(A)\) gilt, müssen \(\mathcal{N}(A)\) und \(\mathcal{R}(A^*)\) orthogonal sein.

Wegen der Dimensionsformel wissen wir, dass gilt

\[\dims\Kern(A) + \dims\Image(A^*) \ = \ n,\]

und daher muss schon \(\Image(A^*) = \mathcal{N}(A)^\perp\) gelten. Diese Identität gilt allgemein für lineare Operatoren, also folgt auch \(\Image(A^*A) = \mathcal{N}(A^*A)^\perp\). Schließlich ergibt sich somit die Identität

\[\begin{aligned} \Image(A^*) \: = \: \Kern(A)^\perp \: = \: \Kern(A^*A)^\perp \: = \: \Image(A^*A). \end{aligned}\]

◻

Mit Hilfe der obigen Eigenschaften lässt sich nun ein Zusammenhang zwischen dem linearen Ausgleichsproblem und den Gaußschen Normalengleichungen herstellen.

Satz 3.1 (Gaußsche Normalengleichungen)

Sei \(A \in \mathbb{R}^{m\times n}\) und \(b \in \mathbb{R}^m\). Ein Vektor \(\hat{x} \in \R^n\) löst genau dann die Gaußschen Normalengleichungen

(3.4)\[A^TA\hat{x} \ = \ A^Tb\]

falls es das linearen Ausgleichsproblem (3.2) löst.

Proof.  
Für \(A= 0\) ist die Aussage trivial. Wir nehmen also an, dass \(A\neq 0\) gilt.
Schritt 1:
Es sei zunächst \(\hat{x} \in \R^n\) eine Lösung des linearen Ausgleichsproblems (3.2). Unter Ausnutzung von Lemma 3.1 haben wir

\[\K^m \ = \ \Image(A) \oplus \Image(A) ^\perp \ = \ \Image(A) \oplus \Kern(A^*)\]

und daher können wir den Vektor \(b \in \K^m\) darstellen als

\[b \ = \ b_\Image + b_\Kern \quad \text{ mit } \quad b_\Image\in \Image(A) \ \text{ und } \ b_\Kern\in \Kern(A^*).\]

Wir zeigen zunächst, dass \(A\hat{x} = b_\Image\) gilt. Da \(b_\Image \in \Image(A)\) im Bild liegt, existiert mindestens ein \(\tilde{x} \in \K^n\) mit \(A\tilde{x} = b_\Image\). Für beliebiges \(x\in\K^n\) gilt dann:

\[\begin{aligned} \norm{b-Ax}_2^2 \ &= \ \norm{b_\Image + b_\Kern - Ax}_2^2 \ = \ \norm{A\tilde{x} + b_\Kern - Ax}_2^2 \ = \ \norm{A\underbrace{(\tilde{x}-x)}_{=: z} + b_\Kern}_2^2\\ \ &= \ \norm{Az -b_\Kern}_2^2 \ = \ \langle Az, Az\rangle - \underbrace{\langle Az,b_\Kern \rangle - \langle b_\Kern, Az \rangle}_{=0} + \, \norm{b_\Kern}_2^2\\ &= \ \norm{Az}^2_2 + \norm{b_\Kern}_2^2. \end{aligned}\]

Hierbei haben wir ausgenutzt, dass \(Az \in \Image(A)\) orthogonal zu \(b_\Kern \in \Kern(A^*)\) ist. Der obige Ausdruck ist minimal genau dann wenn \(Az = 0\), d.h., für solche \(x\in\K^n\) so dass

\[\begin{aligned} \tilde{x} - x \in \Kern(A). \end{aligned}\]

Da \(\hat{x} \in \R^n\) das lineare Ausgleichsproblem (3.2) löst, folgt also, dass

\[\begin{aligned} A\hat{x} \: = \: A\hat{x} + \underbrace{A(\tilde{x} - \hat{x})}_{=0} \: = \: A\tilde{x} \: = \: b_\Image. \end{aligned}\]

Wegen \(A^* b_\Kern = 0\) gilt dann insgesamt

\[A^* b \ = \ A^*(b_\Image + b_\Kern) \ = \ A^* b_\Image \ = \ A^* A\hat{x}.\]

Das heißt \(\hat{x}\) ist Lösung der Normalengleichung (3.4).
Schritt 2:
Sei nun umgekehrt \(\hat{x} \in \mathbb{R}^n\) eine Lösung der Gaußschen Normalengleichungen (3.4). Dann wissen wir, dass das Residuum \(A\hat{x} - b\) im Kern der Matrix \(A^*\) liegen muss, denn es gilt

\[A^*A\hat{x} \ = \ A^*b \quad \Leftrightarrow \quad A^*(A\hat{x}-b) \ = \ 0 \quad \Leftrightarrow \quad A\hat{x}-b \in \mathcal{N}(A^*).\]

Für beliebiges \(x\in \mathbb{R}^n\) definieren wir

\[z \ \coloneqq \ A(x-\hat{x}) \in \mathcal{R}(A), \quad r \ \coloneqq \ b - A\hat{x} \in \mathcal{N}(A^*),\]

so gilt wegen der Orthogonalität \(\langle r,z \rangle = 0\)

\[\norm{b - Ax}_2^2 \ = \ \norm{r - z}_2^2 \ = \ \norm{r}^2_2 - \underbrace{\langle r,z \rangle - \langle z,r \rangle}_{=0} + \, \norm{z}^2_2 \ \geq \ \norm{r}_2^2 \ = \ \norm{b - A\hat{x}}^2_2.\]

Damit haben wir gezeigt, dass

\[\begin{aligned} \norm{b - Ax}_2^2 \ \geq \ \norm{b - A\hat{x}}_2^2\quad\forall x\in\K^n. \end{aligned}\]

Somit ist \(\hat{x} \in \R^n\) eine Lösung des linearen Ausgleichsproblems (3.2)normalen. ◻

In obigen Beweis haben wir für \(A\tilde{x} = b_\Image\) die Identität

\[\begin{aligned} \norm{b- Ax}_2 = \norm{A(\tilde{x} - x)}_2 + \norm{b_\Kern}_2 \end{aligned}\]

gezeigt. Somit sehen wir, dass (3.2) stets mindestens eine Lösung, nämlich \(\hat{x}\) hat. Für den Fall das \(\Kern(A)=\{0\}\) existiert genau ein \(\hat{x} \in \R^n\), so dass \(A\tilde{x} = b_\Image\) gilt und dieses \(\hat{x}\) ist dann auch die eindeutige Lösung des Problems. Dies ist der Inhalt des folgenden Korollars.

Korollar 3.1

Für eine Matrix \(A\in\K^{m\times n}\) mit \(\Kern(A)=\{0\}\) gibt es genau eine Lösung des linearen Ausgleichsproblems (3.2), die auch gleicheztig die eindeutige Lösung der Gaußschen Normalengleichungen (3.4) ist.

Bemerkung 3.2 (Singulärer Fall der Normalengleichungen)

Falls die Matrix \(A^*A\) singulär ist, d.h. \(\Kern(A)\neq\{0\}\) so haben die Gaußschen Normalengleichungen keine eindeutige Lösung und es existieren mehrere Vektoren \(\hat{x} \in \mathbb{R}^n\) für die gilt

\[\begin{aligned} A^*A\hat{x} \, = \, A^* b. \end{aligned}\]

Bemerkung 3.3

Für die Hinrichtung im Beweis von Satz 3.1 gibt es folgenden alternativen Weg für \(\K=\R\). Wir betrachten die Funktion \(\phi:\R^n \to \R\),

\[\begin{aligned} \phi(x) \ \coloneqq \ \frac{1}{2}\norm{b - Ax}_2^2 \ = \ \frac{1}{2} \norm{b}_2^2 - \langle A^*b, x\rangle + \frac{1}{2} \langle A^*Ax, x\rangle, \end{aligned}\]

für welche wir für das lineare Ausgleichsproblem (3.2) ein Minimum \(\hat{x} \in \R^n\) finden wollen. Eine notwendige Bedingung für ein Minimum ist hier gegeben durch

\[\begin{aligned} \nabla \phi(\hat{x}) \: = \: 0. \end{aligned}\]

Um den Gradienten der Funtkion \(\phi\) zu berechnen, nutzen wir, dass für zwei Funktionen \(f,g:\R^n\to\R^m\) gilt

\[\begin{aligned} \nabla\ \langle f(x), g(x)\rangle \ = \ (D f)(x)\cdot g(x) + (D g)(x)\cdot f(x), \end{aligned}\]

wobei \(D f, D g\) die Jacobi-Matrizen der entsprechenden Funktionen bezeichnen. Damit sehen wir, dass

\[\begin{aligned} \nabla \phi(x) \ &= \ \underbrace{\nabla \frac{1}{2} \norm{b}_2^2}_{=0} - \nabla \langle A^*b, x\rangle + \frac{1}{2} \nabla \langle A^*Ax, x\rangle\\ \ &= \ -\underbrace{(\nabla (A^*b))}_{=0} x - \underbrace{(\nabla (x))}_{=I} A^*b+ \frac{1}{2} \underbrace{(\nabla (A^*Ax))}_{=A^*A} x+ \frac{1}{2} \underbrace{(\nabla (x))}_{=I} A^*Ax\\ \ &= \ -A^*b + A^*A x. \end{aligned}\]

Somit wissen wir, dass ein Minimum \(\hat{x}\in \R^n\) von \(\phi\) die Gleichung

\[\begin{aligned} A^*A x - A^*b \: = \: 0 \quad \Leftrightarrow \quad A^*b \: = \: A^*A x \end{aligned}\]

also die Normalengleichung erfüllt.

Beispiel 3.3

Die Matrix \(A\) des Experiments aus Beispiel 3.1 und die rechte Seite \(b\) der Messdaten hatten die Form

\[\begin{aligned} A = \begin{pmatrix} 5&1\\ 6& 1\\ 8& 1\\ 9& 1\\ 11&1\\ 16&1\\ 30&1\\ 23&1 \end{pmatrix}, \qquad % b = \begin{pmatrix} 2\\7\\4\\18\\12\\22\\89\\32 \end{pmatrix}. % \end{aligned}\]

Die Normalengleichung führt in diesem Fall dann auf

\[\begin{aligned} A^T A x \: = \: A^T b \quad \Leftrightarrow \quad \begin{pmatrix} 2012 & 108\\108 &8 \end{pmatrix} % x \: = \: \begin{pmatrix} 4136\\186 \end{pmatrix}, \end{aligned}\]

was als Lösung den Parametervektor \(\hat{p}\approx (2.9,-16.3)^T\) aus Beispiel 3.2 hat. Die Norm des Residuums beträgt hier

\[\begin{aligned} \norm{b - A\hat{p}}_2 \ = \ \sqrt{\sum_{i=1}^N \abs{t_i - (\hat{p}_1 n_i +\hat{p}_0)}^2} \ \approx \ 29.6, \end{aligned}\]

welches ebenfalls in Abb. 3.2 visualisiert ist.

3.1.3. Normalengleichung und Singulärwertzerlegung

Zum Abschluss diskutieren wir noch eine Darstellung der Lösung der Normalengleichung für eine Matrix \(A\in\R^{m\times n}\) mit Hilfe der Singulärwertzerlegung \(A=U\Sigma V^T\).

Lemma 3.2 (Lösung der Normalengleichungen mit SVD)

Für eine Matrix \(A\in\R^{m\times n}\) betrachten wir die Singulärwertzerlegung \(A=U\Sigma V^T\), wobei \(V \in \R^{n \times n}\) und \(U \in \R^{m \times m}\) orthogonale Matrizen sind und \(\Sigma\in\R^{m\times n}\) eine Nullmatrix ist, auf deren Diagonale die \(r \leq \min\lbrace m,n\rbrace\) Singulärwerte \(\sigma_1\geq \ldots\geq \sigma_r >0\) von A stehen. Hier ist die Lösung der Normalengleichung gegeben durch:

\[\begin{aligned} x \: = \: V\Sigma^{-1} U^T b. \end{aligned}\]

Hierbei bezeichnen wir mit \(\Sigma^{-1}\in\R^{n\times m}\) eine Nullmatrix für deren Diagonalelemente gilt:

\[\begin{aligned} \left(\Sigma^{-1}\right)_{ii} \ = \ \begin{cases} \frac{1}{\sigma_i}&\text{ für } i=1,\ldots,r,\\ 0 &\text{ sonst}. \end{cases} \end{aligned}\]

Proof. Sei \(x \in \R^n\) eine Lösung der Normalengleichungen \(A^TAx = A^T b\). Dann können wir mit Hilfe der Singulärwertzerlegung \(A = U \Sigma V^T\) von \(A\) folgern:

\[\begin{aligned} &\qquad A^TAx \ = \ A^Tb\\ \Leftrightarrow& \qquad V \Sigma^T \underbrace{U^T U}_{= I_n} \Sigma V^T x \ = \ V \Sigma U^T b\\ \Leftrightarrow& \qquad V \Sigma^2 V^T x \ = \ V \Sigma U^T b\\ \Leftrightarrow& \qquad V^T x \ = \ \ \underbrace{(\Sigma^2)^{-1} \Sigma}_{=: \, \Sigma^{-1}} U^T b\\ \Leftrightarrow& \qquad x \ = \ V \Sigma^{-1} U^T b. \end{aligned}\]

◻

Die Singulärwertzerlegung erlaubt uns auch eine einfache Analyse der Kondition des Matrixproduktes \(A^TA\) der Normalengleichungen in der Spektalnorm. Wir nehmen im Folgenden an, dass \(\Kern(A)=\{0\}\) gilt und somit \(r=n\) ist, da wir den überbestimmten Fall mit \(m>n\) diskutieren. Für die Kondition gilt dann wegen Bemerkung 2.7 und Beispiel 2.10

\[\begin{aligned} \kappa_2(A^TA) \: = \: \frac{\sigma_1^2}{\sigma_n^2}, \end{aligned}\]

wobei \(\sigma_1 \in \R^+\) den größten Singulärwert von \(A\) und \(\sigma_n \in \R^+\) den kleinsten Singulärwert von \(A\) darstellt. Im Fall einer regulären \(n\times n\) Matrix ist dies also das Quadrat der Kondition von \(A\).

Für einen beliebigen Vektor \(y \in \R^n\) bekommen wir nach Satz 2.4 für eine lineares Gleichungssystem der Form \(A^T A x = y\) also nur die folgende grobe Abschätzung für den relativen Fehler in der Lösung \(x \in \R^n\):

\[\begin{aligned} \delta_x^{\text{rel}} \: \leq \: \frac{\sigma_1^2}{\sigma_n^2} \cdot \frac{\norm{\Delta_y}}{\norm{y}}. \end{aligned}\]

Somit könnten wir erwarten, dass die Normalengleichung deutlich schlechter konditioniert ist als das ursprüngliche Gleichungssystem.

Dies stimmt aber nur bedingt, wie wir aus einem einfachen Argument sehen. Wenn die Störung nur in der rechten Seite \(b \in \R^m\) der Normalengleichungen vorliegt, so ist die Differenz der Lösung

\[\begin{aligned} x- \tilde x \: = \: V \Sigma^{-1} U^T (b-\tilde b). \end{aligned}\]

Damit gilt nach Lemma 3.2 für den relativen Fehler

\[\begin{aligned} \delta_x^{\text{rel}} \: = \: \frac{x- \tilde{x}}{||x||} \: = \: \frac{\Vert V \Sigma^{-1} U^T (b-\tilde b) \Vert}{\Vert V \Sigma^{-1} U^T b \Vert} \: = \: \frac{\Vert \Sigma^{-1} U^T (b-\tilde b) \Vert}{\Vert \Sigma^{-1} U^T b \Vert}, \end{aligned}\]

wobei wir ausgenutzt haben, dass \(V\) eine orthogonale Matrix ist. Da aber für die Diagonaleinträge der Matrix \(\Sigma^{-1}\) gilt

\[\begin{aligned} \frac{1}{\sigma_1} \: \leq \: (\Sigma^{-1})_{ii} \: \leq \: \frac{1}{\sigma_n}, \quad i=1,\ldots,n, \end{aligned}\]

folgt für einen beliebigen Vektor \(z\in\R^{m}\)

\[\begin{aligned} \frac{1}{\sigma_1} \norm{z} \: \leq \: \norm{\Sigma^{-1} z} \: \leq \: \frac{1}{\sigma_n} \norm{z}. \end{aligned}\]

Daraus folgern wir, dass gilt

\[\begin{aligned} \delta_x^{\text{rel}} \: = \: \frac{\Vert x - \tilde x\Vert}{\Vert x \Vert} \: \leq \: \frac{\sigma_1}{\sigma_n} \cdot \frac{\Vert U^T( b-\tilde b )\Vert}{\Vert U^T b \Vert} \: = \: \frac{\sigma_1}{\sigma_n} \cdot \frac{\Vert b-\tilde b \Vert}{\Vert b \Vert} \: = \: \frac{\sigma_1}{\sigma_n} \cdot \frac{\Vert \Delta_b \Vert}{\Vert b \Vert}. \end{aligned}\]

Also erhalten wir mit dieser verbesserten Fehlerabschätzung doch nur \(\sqrt{\kappa_2(A^T A)}\) als maßgeblichen Faktor und nicht \(\kappa_2(A^T A)\) wie oben gefolgert. Der Grund dafür ist, dass wir bei der Normalengleichung nicht eine beliebige rechte Seite haben, sondern sehr speziell \(y=A^T b\).

Bemerkung 3.4 (Störung in der Matrix)

Die Situation ändert sich, wenn wir auch Fehler in der Matrix \(A\) zulassen. Dann haben wir eine Gleichung der Form

\[\begin{aligned} \tilde A^T \tilde A (x-\tilde x) = (\tilde A^T \tilde A - A^T A) x + \tilde A^T \tilde b - A^T b, \end{aligned}\]

und es gibt keinen Grund warum die rechte Seite als Produkt von \(\tilde A^T\) mit einem Fehler von Interesse dargestellt werden können soll. In diesem Fall ist also \(\kappa_2(A^T A)\) der maßgebliche Faktor für die Fehlerabschätzung und wir sehen, dass die Normalengleichungen deutlich sensitiver gegenüber einem Fehler in der Matrix sind als gegenüber einem Fehler in der rechten Seite.