6.2. Numerische Integration mit unterschiedlichen Schrittweiten

Bisher haben wir interpolatorische Quadraturformeln für die numerische Integration hergeleitet, die auf einer festen Schrittweite \(h > 0\) und \(n \in \N_+\) Stützpunkten basierten. Wir haben bereits im letzten Abschnitt festgestellt, dass dies für \(n \geq 8\) zu Instabilitäten führt. Der Grund hierfür ist, dass das Interpolationspolynom durch die Wahl von äquidistanten Stützstellen eine beliebig große Abweichung von der zu Grunde liegenden Funktion haben kann im Sinne der Maximumsnorm (vergleiche Beispiel 5.5).

Aus diesem Grund wollen wir in diesem Abschnitt Ingegrationsformeln mit unterschiedlichen Schrittweiten \(h >0\) konstruieren, deren Approximationsfehler mit einer hohen Potenz von \(h\) abfallen. Im Speziellen widmen wir uns dem Romberg-Verfahren, das im Wesentlich auf der Trapezregel basiert.

6.2.1. Euler-Maclaurinsche Summenformel

Wir beginnen zunächst mit einer zentralen Idee, die wir als Grundlage für die numerische Integration mit verschiedenen Schrittweiten nutzen wollen, der Euler-Maclaurinschen Summenformel. Ursprünglich leitete Euler sich diese Formel her zur Berechnung einer Summe von Funktionswerten durch die Werte der Ableitungen dieser Funktion an den Summationsgrenzen. Maclaurin wandelte sie dann später ab für die numerische Approximation eines bestimmten Integrals über einzelne Werte des Integranden und seiner Ableitungen.

Zur Formulierung der Euler-Maclaurinschen Summenformel benötigen wir zunächst die Definition sogenannter Bernoulli-Polynome und Bernoulli-Zahlen. Diese tauchen in unterschiedlichen Gebieten der Mathematik auf und spielen beispielsweise bei der Riemannschen Zetafunktion ebenfalls eine wichtige Rolle.

Wir wollen zunächst die grundlegenden Bernoulli-Polynome und die damit eng verknüpften Bernoulli-Zahlen einführen.

Definition 6.2 (Bernoulli-Polynome und Bernoulli-Zahlen)

Sei \(n \in \N\), dann ist das Bernoulli-Polynom \(\mathrm{B_n} \in \Pi_n\) mit \(\mathrm{B_n} \colon [0,1] \rightarrow \R\) durch folgende Rekursionsgleichungen

(6.5)\[\begin{split} \mathrm{B_0}(x) \ &\coloneqq \ 1\\ \mathrm{B'_{n+1}}(x) \ &\coloneqq \ (n+1) \cdot \mathrm{B_n}(x), \end{split}\]

und die zusätzliche Integralbedingung

(6.6)\[\int_0^1 \mathrm{B_n}(x) \, \mathrm{d}x \ = \ 0, \qquad n \geq 1\]

vollständig charakterisiert.

Wir definieren die Bernoulli-Zahlen (erster Art) \(B_n \in \R\) als konstante Terme der Bernoulli-Polynome \(\mathrm{B_n}(x) \in \Pi_n\), d.h. wir setzen

\[B_n \ \coloneqq \ \mathrm{B_n}(0).\]

Das folgende Beispiel gibt die ersten Bernoulli-Polynome explizit an und zeigt, dass die Bedingungen in Definition 6.2 diese schon eindeutig festlegen.

Beispiel 6.5 (Erste Bernoulli-Polynome)

Wir wollen im Folgenden die ersten Bernoulli-Polynome \(\mathrm{B_n}(x) \in \Pi_n\) für \(n = 0,\ldots,6\) aus den Rekursionsgleichungen (6.5) und der Integralbedingung (6.6) berechnen.

Das erste Bernoulli-Polynom \(\mathrm{B_0}\) für \(n=0\) ist per Definition gegeben und es gilt \(\mathrm{B_0}(x) \equiv 1\) für \(x \in [0,1]\).

Für \(n=1\) müssen wir nun die folgende Rekursionsbedingung erfüllen

\[\mathrm{B'_1}(x) \ = \ 1 \cdot \mathrm{B_0}(x) \ = \ 1.\]

Daraus folgt, dass das Bernoulli-Polynom \(\mathrm{B_1}(x)\) die Form \(\mathrm{B_1}(x) = x + c\) mit einer unbestimmten Integrationskonstante \(c \in \R\) haben muss. Zur Bestimmung von \(c\) wenden wir nun die zusätzliche Bedingung (6.6) an, die besagt, dass für Bernoulli-Polynome gelten muss:

\[0 \ = \ \int_0^1 \mathrm{B_1}(x) \, \mathrm{d}x \ = \ \int_0^1 x + c \, \mathrm{d}x \ = \ \left[ \frac{1}{2}x^2 + cx \right]_0^1 \ = \ \frac{1}{2} + c.\]

Daraus folgt direkt, dass \(c = -\frac{1}{2}\) sein muss und somit hat das Bernoulli-Polynom \(\mathrm{B_1}\) die Form

\[\mathrm{B_1}(x) \ = \ x - \frac{1}{2}.\]

Dieses Vorgehen kann man nun sukzessive weiter anwenden und erhält so die ersten Bernoulli-Polynome für \(n = 0,\ldots,6\) durch:

\[\begin{split} \mathrm{B_0}(x) \ &= \ 1,\\ \mathrm{B_1}(x) \ &= \ x - \frac{1}{2},\\ \mathrm{B_2}(x) \ &= \ x^2 - x + \frac{1}{6},\\ \mathrm{B_3}(x) \ &= \ x^3 - \frac{3}{2}x^2 + \frac{1}{2}x,\\ \mathrm{B_4}(x) \ &= \ x^4 - 2x^3 + x^2 - \frac{1}{30},\\ \mathrm{B_5}(x) \ &= \ x^5 - \frac{5}{2}x^4 + \frac{5}{3}x^3 - \frac{1}{6}x,\\ \mathrm{B_6}(x) \ &= \ x^6 - 3x^5 + \frac{5}{2}x^4 - \frac{1}{2}x^2 + \frac{1}{42}. \end{split}\]

Abb. 6.1 visualisiert die Bernoulli-Polynome \(\mathrm{B_n}\) für \(n=1,\ldots,6\) auf dem Intervall \([0,1]\).

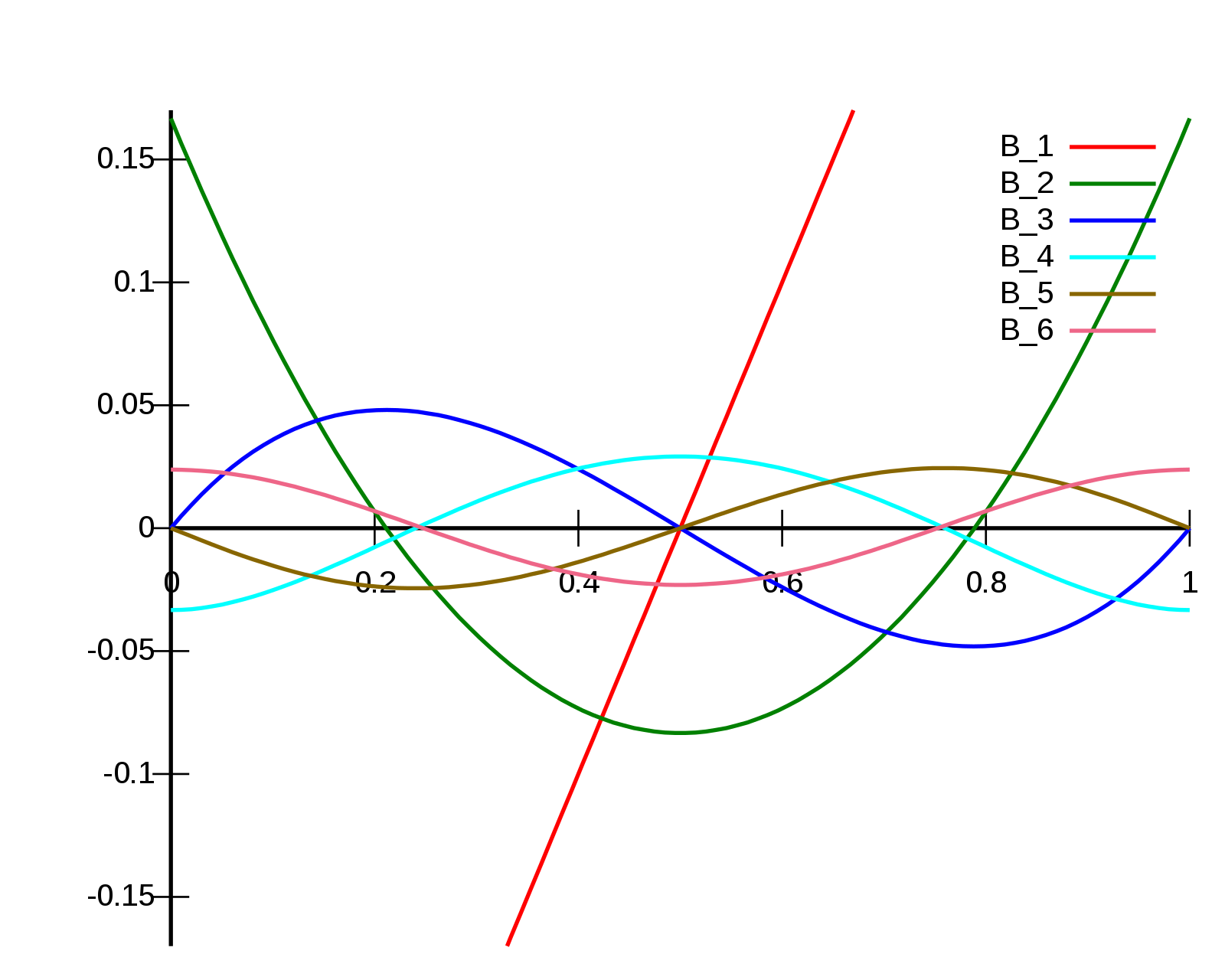
Abb. 6.1 Visualisierung der Bernoulli-Polynome \(\mathrm{B_n}\) vom Grad \(1\) bis \(6\) auf dem Intervall \([0,1]\) [Ber]

Bemerkung 6.6 (Alternative Definition von Bernoulli-Polynomen)

In der Literatur werden Bernoulli-Polynome anstatt durch die Integralbedingung (6.6) manchmal auch durch eine alternative Randbedingung beschrieben. Hierbei fordert man, dass die konstanten Terme der Bernoulli-Polynome ungeraden Grades verschwinden, d.h. es soll gelten

(6.7)\[\mathrm{B_{2n+1}}(0) \ = \ \mathrm{B_{2n+1}}(1) \ = \ 0, \qquad n \in \N_+.\]

Diese Bedingung lässt sich als Eigenschaft ebenfalls aus der Integralbedingung (6.6) folgern (siehe Lemma 6.1).

Für ein gegebenes Polynom \(\mathrm{B_{2n-1}}\) ist \(\mathrm{B_{2n}}\) durch die Rekursionsbedingung (6.5) bis auf eine additive Integrationskonstante eindeutig bestimmt. Diese lässt sich durch die zusätzliche Randbedingung (6.7)für Bernoulli-Polynome \(\mathrm{B_{2n+1}}\) von ungeradem Grad eindeutig bestimmen. Um dies zu verstehen betrachten wir zunächst für \(n \in \N_+\) das allgemeine Bernoulli-Polynom

\[\mathrm{B_{2n-1}}(x) \ = \ x^{2n-1} + c_{2n-2}x^{2n-2} + \ldots + c_1x + c_0\]

mit bekannten Koeffizienten \(c_0,\ldots, c_{2n-2} \in \R\). Durch Integration und unter Einhaltung der Rekursionsbedingung (6.5) folgt dann, dass

\[\mathrm{B_{2n}}(x) \ = \ x^{2n} + \frac{2n}{2n-1} \cdot c_{2n-2}x^{2n-1} + \ldots + \frac{2n}{2}c_1x^2 + 2nc_0x + c\]

mit einer noch unbestimmten Integrationskonstante \(c\in \R\) gilt. Unter Verwendung des gleichen Arguments erhalten wir durch nochmalige Integration

\[\mathrm{B_{2n+1}}(x) \ = \ x^{2n+1} + \frac{(2n+1)2n}{2n(2n-1)} c_{2n-2}x^{2n} + \ldots + \frac{(2n+1)2n}{3\cdot 2}c_1x^3 + \frac{(2n+1)2n}{2}c_0x^2 + (2n+1)cx + d\]

mit unbestimmten Integrationskonstanten \(c,d \in \R\). Wendet man nun die zusätzliche Randbedingungen (6.7) an, so erhält man zunächst, dass wegen \(\mathrm{B_{2n+1}}(0) = 0\) schon \(d = 0\) gelten muss. Die Integrationskonstante \(c\) ist ebenfalls eindeutig bestimmt, denn wir können aus der Bedingung \(\mathrm{B_{2n+1}}(1) = 0\) und \(d=0\) einfach berechnen:

\[\begin{split} 0 \ &\overset{!}{=} \ 1 + \frac{(2n+1)2n}{2n(2n-1)} c_{2n-2} + \ldots + + \frac{(2n+1)2n}{3\cdot 2}c_1 + \frac{(2n+1)2n}{2}c_0 + (2n+1)c\\ \Rightarrow \quad c \ &= \ - \frac{1 + \frac{(2n+1)2n}{2n(2n-1)} c_{2n-2} + \ldots + \frac{(2n+1)2n}{3\cdot 2}c_1 + \frac{(2n+1)2n}{2}c_0 }{2n+1}. \end{split}\]

Aus diesem Grund sind Bernoulli-Polynome durch die Bedingungen in (6.7) ebenfalls vollständig charakterisiert.

Die folgende Bemerkung nennt weitere Darstellungsformen der Bernoulli-Polynome aus verschiedenen mathematischen Gebieten.

Bemerkung 6.7 (Darstellung von Bernoulli-Polynomen und -zahlen)

Bernoulli-Polynome tauchen in sehr unterschiedlichen mathematischen Teilgebieten auf, z.B. in der algebraischen Zahlentheorie, in der Kombinatorik oder der algebraischen Topologie. Daher gibt es auch alternative Darstellungsformen als die in Definition 6.2 gegebene, wie wir im Folgenden festhalten wollen.

1. Man kann zeigen, dass sich das \(n\)-te Bernoulli-Polynom \(\mathrm{B_n} \in \Pi_n\) durch folgenden geschlossenen Ausduck rekursiv berechnen lässt:

   \[\mathrm{B_n}(x) \ = \ \sum_{k=0}^n \begin{pmatrix}n\\k\end{pmatrix} B_k x^{n-k},\]

   wobei \(B_k \in \R\) hier die Bernoulli-Zahlen (erster Art) aus Definition 6.2 bezeichnen.

   Auf Grund der Rekursionsbeziehung (6.5) lassen sich die Bernoulli-Zahlen \(B_n \in \R\) für den Startwert \(B_0 \coloneqq 1\) ebenfalls rekursiv wie folgt berechnen:

   (6.8)\[B_n \ \coloneqq \ - \frac{1}{n+1} \sum_{k=0}^{n-1} \begin{pmatrix} n+1\\ k \end{pmatrix} B_k.\]

2. Die Bernoulli-Zahlen \(B_n \in \R\) lassen sich mit Hilfe einer generierenden Funktion implizit definieren als Koeffizienten der folgenden Reihendarstellung

   \[\frac{x}{e^x - 1} \ = \ \sum_{k=0}^\infty B_k \frac{x^k}{k!}.\]

   Daraus lässt sich ein ähnlicher Zusammenhang für die Bernoulli-Polynome \(\mathrm{B_n} \in \Pi_n\) ableiten, denn es gilt für \(x,t \in \R\):

   \[\frac{te^{tx}}{e^t - 1} \ = \ \sum_{k=0}^\infty \mathrm{B_k}(x) \frac{t^k}{k!}.\]

Wir wollen im Folgenden die ersten drei Bernoulli-Zahlen mit Hilfe der Rekursionformel in (6.8) explizit berechnen.

Beispiel 6.6 (Bernoulli-Zahlen)

Wir wollen in diesem Beispiel die ersten drei Bernoulli-Zahlen \(B_1, B_2, B_3 \in \R\) explizit mittels Rekursion berechnen. Für \(n=1\) berechnen wir die einzige Bernoulli-Zahl mit ungeradem Index \(B_1 \neq 0\) als:

\[B_1 \ = \ - \frac{1}{2} \cdot \begin{pmatrix}2\\ 0\end{pmatrix} B_0 \ = \ -\frac{1}{2} \cdot \frac{2!}{0! \cdot 2!} \cdot 1 \ = \ \mathbf{- \frac{1}{2}}\]

Für \(n=2\) berechnen wir mit Hilfe der vorigen Bernoulli-Zahlen \(B_0, B_1\) die Bernoulli-Zahl \(B_2 \in \R\) als:

\[\begin{split} B_2 \ &= \ - \frac{1}{3} \cdot \left[ \begin{pmatrix}3\\ 0\end{pmatrix} B_0 + \begin{pmatrix}3\\ 1\end{pmatrix} B_1 \right] \ = \ -\frac{1}{3} \cdot \left[ \frac{3!}{0! \cdot 3!} \cdot 1 - \frac{3!}{1! \cdot 2!} \cdot \frac{1}{2}\right] \\ &= \ -\frac{1}{3} \cdot \left[ 1 - \frac{3}{2} \right] \ = \ \mathbf{\frac{1}{6}}. \end{split}\]

Für \(n=3\) berechnen wir mit Hilfe der vorigen Bernoulli-Zahlen \(B_0, B_1, B_2\) die Bernoulli-Zahl \(B_3 \in \R\) als:

\[\begin{split} B_3 \ &= \ - \frac{1}{4} \cdot \left[ \begin{pmatrix}4\\ 0\end{pmatrix} B_0 + \begin{pmatrix}4\\ 1\end{pmatrix} B_1 + \begin{pmatrix}4\\ 2\end{pmatrix} B_2 \right] \\ &= \ -\frac{1}{4} \cdot \left[ \frac{4!}{0! \cdot 4!} \cdot 1 - \frac{4!}{1! \cdot 3!} \cdot \frac{1}{2} + \frac{4!}{2! \cdot 2!} \cdot \frac{1}{6} \right] \\ &= \ -\frac{1}{4} \cdot \left[ 1 - 2 + 1 \right] \ = \ \mathbf{0}. \end{split}\]

Das folgende Hilfslemma formuliert wichtige Eigenschaften der Bernoulli-Polynome, die für den Beweis von Satz 6.3 entscheidend sein werden.

Lemma 6.1 (Eigenschaften der Bernoulli-Polynome)

Wir können die folgenden Eigenschaften für die Bernoulli-Polynome \(\mathrm{B_n} \in \Pi_n\) festhalten.

1. Für \(n\in\N, n \geq 2\) gelten für das Bernoulli-Polynom \(\mathrm{B_n}\) die Randbedingungen

   (6.9)\[\mathrm{B_n}(1) \ = \ \mathrm{B_n}(0) \ = \ B_n,\]

   wobei \(B_n\) die \(n\)-te Bernoulli-Zahl bezeichnet.

2. Für \(n\in\N_+\) gilt das folgende Umbral-Kalkül für das Bernoulli-Polynom \(\mathrm{B_n}\):

   \[F_n(x) \ := \ \mathrm{B_n}(x+1) - \mathrm{B_n}(x) \ = \ n \cdot x^{n-1}.\]

3. Falls \(P \in \Pi_n\) für \(n \in \N\) ein Polynom mit der Eigenschaft aus \((\text{ii})\) ist, d.h. es gilt

   \[P(x+1) - P(x) \ = \ n \cdot x^{n-1},\]

   so ist \(P\) schon von der Form \(P(x) = \mathrm{B_n}(x) + c\) mit einer Konstanten \(c \in \R\).

4. Für \(n\in\N\) gilt die folgende Symmetriebeziehung für ein Bernoulli-Polynom \(\mathrm{B_n}\):

   \[(-1)^n \mathrm{B_n}(1-x) \ = \ \mathrm{B_n}(x), \qquad \forall \, x \in [0,1].\]

5. Für \(n\in\N_+\) gelten für alle Bernoulli-Polynome von ungeradem Grad \(\mathrm{B_{2n+1}}\) die Randbedingungen

   (6.10)\[\mathrm{B_{2n+1}}(0) \ = \ \mathrm{B_{2n+1}}(1) \ = \ 0.\]

Proof. In der Hausaufgabe zu zeigen. ◻

Mit den obigen Vorüberlegungen zu Bernoulli-Polnomen und -zahlen sind wir nun in der Lage die zentrale Aussage dieses Abschnitts zu formulieren und beweisen.

Satz 6.3 (Euler-Maclaurinsche Summenformel)

Sei \(f \in C^{2m+2}([0,1])\) eine auf dem Intervall \([0,1]\) mindestens \((2m+2)\)-mal stetig differenzierbare Funktion für ein beliebiges \(m \in \N\). Dann existiert ein \(\xi \in (0,1)\), so dass die sogenannte Euler-Maclaurinsche Summenformel gilt:

\[\int_0^1 f(t) \, \mathrm{d}{t} \ = \ \frac{f(0)}{2} + \frac{f(1)}{2} + \sum_{k=1}^m \frac{B_{2k}}{(2k)!} \left( f^{(2k-1)}(0) - f^{(2k-1)}(1)\right) - \frac{B_{2m+2}}{(2m+2)!}f^{(2m+2)}(\xi).\]

Hierbei stellen die Koeffizienten \(B_{2k} \in \R, k=1,\ldots,m+1\) die Bernoulli-Zahlen aus Definition 6.2 dar.

Proof. Zunächst formen wir das bestimmte Integral \(\int_0^1 f(t) \mathrm{d}t\) mit Hilfe der partiellen Integration für das Bernoulli-Polynom \(\mathrm{B_1} \in \Pi_1\) mit \(\mathrm{B_1}(x) \coloneqq x - \frac{1}{2}\) um zu:

\[\int_0^1 f(t) \, \mathrm{d}t \ = \ \int_0^1 \underbrace{\mathrm{B'_1}(t)}_{= \, 1}\cdot f(t) \, \mathrm{d}t \ = \ \Bigl[\mathrm{B_1}(t) \cdot f(t) \Bigr]_0^1 - \int_0^1 \mathrm{B_1}(t) \cdot f'(t) \, \mathrm{d}t\]

Den ersten Term berechnen wir explizit als

(6.11)\[\Bigl[\mathrm{B_1}(t) \cdot f(t) \Bigr]_0^1 \ = \ \left(1 - \frac{1}{2}\right) \cdot f(1) - \left(0 - \frac{1}{2}\right) \cdot f(0) \ = \ \frac{1}{2}(f(0) + f(1)).\]

Wir können das auftretende bestimmte Integral \(\int_0^1 \mathrm{B_1}(t) f'(t) \, \mathrm{d}t\) nun sukzessive weiter durch partielle Integration umformen, indem wir die Rekursioneigenschaft der Bernoulli-Polynome \(\mathrm{B_n}\) in (6.5) ausnutzen. Dadurch erhalten wir die folgenden Identitäten:

(6.12)\[\begin{split} \int_0^1 \mathrm{B_1}(t) \cdot f'(t) \, \mathrm{d}t \ &= \ \int_0^1 \frac{1}{2} \mathrm{B'_2}(t) \cdot f'(t) \, \mathrm{d}t \\ &= \ \frac{1}{2} \Bigl[\mathrm{B_2}(t) \cdot f'(t) \Bigr]_0^1 - \frac{1}{2} \int_0^1 \mathrm{B_2}(t) \cdot f''(t) \, \mathrm{d}t \\ & \hspace{1cm} \vdots\\ \int_0^1 \mathrm{B_{k-1}}(t) \cdot f^{(k-1)}(t) \, \mathrm{d}t \ &= \ \int_0^1 \frac{1}{k} \mathrm{B'_k}(t) \cdot f^{(k-1)}(t) \, \mathrm{d}t \ \\ &= \ \frac{1}{k} \Bigl[\mathrm{B_k}(t) \cdot f^{(k-1)}(t) \Bigr]_0^1 - \frac{1}{k} \int_0^1 \mathrm{B_k}(t) \cdot f^{(k)}(t) \, \mathrm{d}t \\ \end{split}\]

Nun können wir wegen der Randbedingungen (6.9) der Bernoulli-Polynome \(\mathrm{B_k}\) mit \(k>1\) für die Auswertungen der partiellen Integrationen in (6.12) folgern, dass gilt

\[\Bigl[ \frac{1}{k}\mathrm{B_k}(t)f^{(k-1)}(t) \Bigr]_0^1 \ = \ \frac{1}{k}B_k f^{(k-1)}(1) - \frac{1}{k}B_k f^{(k-1)}(0) \ = \ -\frac{B_k}{k}\left(f^{(k-1)}(0) - f^{(k-1)}(1)\right).\]

Wegen der Randbedingung (6.10) wissen wir außerdem, dass für die Bernoulli-Polynome \(\mathrm{B_k}\) von ungeradem Grad \(k\in N\) gilt:

\[\mathrm{B_k}(0) \ = \ \mathrm{B_k}(1) \ = \ 0.\]

Dadurch fallen in (6.12) also alle Terme der Form \(\frac{1}{k} \Bigl[\mathrm{B_k}(t) \cdot f^{(k-1)}(t) \Bigr]_0^1\) für ungerades \(k \in N\) weg und somit lässt sich mit (6.11) die Euler-Maclaurinsche Summenformel nun schreiben als

\[\int_0^1 f(t) \, \mathrm{d}t \ = \ \frac{1}{2}(f(0) + f(1)) + \sum_{k=1}^m \frac{B_{2k}}{(2k)!}\left( f^{(2k-1)}(0) - f^{(2k-1)}(1)\right) + r_{m+1},\]

wobei für das Restglied \(r_{m+1}\) gilt:

\[r_{m+1} \ \coloneqq \ - \frac{1}{(2m+1)!} \int_0^1 \mathrm{B_{2m+1}}(t) f^{(2m+1)}(t) \, \mathrm{d}t.\]

Integrieren wir das Integral des Restglieds \(r_{m+1}\) nochmals partiell erhalten wir für eine spezielle Wahl der Stammfunktion

\[\begin{split} \int_0^1 &\mathrm{B_{2m+1}}(t) f^{(2m+1)}(t) \, \mathrm{d}t \ =\\ &\Bigl[\frac{1}{2m+2}\left( \mathrm{B_{2m+2}}(t) - B_{2m+2}\right)f^{(2m+1)}(t) \Bigr]_0^1 - \frac{1}{2m+2} \int_0^1 (\mathrm{B_{2m+2}}(t) - B_{2m+2}) f^{(2m+2)}(t) \, \mathrm{d}t. \end{split}\]

Der erste Term verschwindet wegen (6.9), so dass für das Restglied insgesamt gilt:

\[r_{m+1} \ = \ \frac{1}{(2m+2)!} \int_0^1 (\mathrm{B_{2m+2}}(t) - B_{2m+2}) f^{(2m+2)}(t) \, \mathrm{d}t\]

Wir können das Restglied \(r_{m+1}\) weiter vereinfachen, wenn wir annehmen, dass die Hilfsfunktion

\[g(t) \ \coloneqq \ \mathrm{B_{2m+2}}(t) - B_{2m+2}\]

auf dem Intervall \([0,1]\) nicht das Vorzeichen wechselt, d.h., es gilt entweder die Bedingung \(g(t) \geq 0\) oder die Bedingung \(g(t) \leq 0\) für alle \(t \in [0,1]\). Das dem wirklich so ist, werden wir im Anschluss in Lemma 6.2 beweisen.

Nun können wir den Mittelwertsatz der Integralrechnung anwenden und damit das Restglied wie folgt für ein \(\xi \in [0,1]\) vereinfachen:

\[\begin{split} r_ {m+1} \ &= \ \frac{1}{(2m+2)!} \int_0^1 (\mathrm{B_{2m+2}}(t) - B_{2m+2}) f^{(2m+2)}(t) \, \mathrm{d}t \ = \ \frac{1}{(2m+2)!} \int_0^1 g(t) f^{(2m+2)}(t) \, \mathrm{d}t \\ &= \ \frac{f^{(2m+2)}(\xi)}{(2m+2)!} \int_0^1 g(t) \, \mathrm{d}{t} \ = \ \frac{f^{(2m+2)}(\xi)}{(2m+2)!} \int_0^1 \mathrm{B_{2m+2}}(t) - B_{2m+2} \, \mathrm{d}{t}\\ &= \ - \frac{B_{2m+2}}{(2m+2)!}f^{(2m+2)}(\xi) + \frac{f^{(2m+2)}(\xi)}{(2m+2)!} \cdot \int_0^1 \mathrm{B_{2m+2}}(t) \, \mathrm{d}{t} \end{split}\]

für ein \(\xi \in [0,1]\). Wegen der Integrationseigenschaft der Bernoulli-Polynome in Lemma 6.1 verschwindet das Integral und somit gilt für das Restglied insgesamt

\[r_{m+1} \ = \ -\frac{B_{2m+2}}{(2m+2)!} f^{(2m+2)}(\xi), \qquad \xi \in [0,1].\]

Damit haben wir die Euler-Maclaurinsche Summenformel schließlich bewiesen und es gilt insgesamt für ein \(\xi \in [0,1]\):

\[\int_0^1 f(t) \, \mathrm{d}t \ = \ \frac{1}{2}(f(0) + f(1)) + \sum_{k=1}^m \frac{B_{2k}}{(2k)!}\left( f^{(2k-1)}(0) - f^{(2k-1)}(1)\right) - \frac{B_{2m+2}}{(2m+2)!} f^{(2m+2)}(\xi).\]

◻

Zur Vervollständigung des Beweises der Euler-Maclaurinschen Summenformel müssen wir noch folgendes Lemma über das Vorzeichen von Bernoulli-Polynome und Bernoulli-Zahlen formulieren.

Lemma 6.2 (Vorzeichen von Bernoulli-Polynomen und -zahlen)

Sei \(n \in \N_+\) und \(\mathrm{B_n} \in \Pi_n\) und \(B_n \in \R\) seien das entsprechende Bernoulli-Polynom bzw. die entsprechende Bernoulli-Zahl. Dann gelten die folgenden Vorzeicheneigenschaften:

1. \((-1)^n \mathrm{B_{2n-1}}(x) > 0\)   für \(0 < x < \frac{1}{2}\),

2. \((-1)^n (\mathrm{B_{2n}}(x) - B_{2n}) > 0\) für \(0 < x < 1\),

3. \((-1)^{n+1} B_{2n} > 0\).

Proof. In der Hausaufgabe zu zeigen. ◻

Aus der Euler-Maclaurinschen Summenformel in Satz 6.3 lassen sich direkt Verfahren zur numerischen Approximation des bestimmten Integrals einer Funktion \(f\) ableiten, wie das folgende Korollar zeigt.

Korollar 6.2 (Einfache Interpolationsformel mit Ableitungen)

Für \(m=1\) erhalten wir für eine Funktion \(f \in C^1([a,b])\) folgende Approximation des bestimmten Integrals auf dem Intervall \([0,1] \subset \R\):

(6.13)\[\begin{split} \int_0^1 f(t) \, \mathrm{d}t \ &\approx \ \frac{1}{2} (f(0) + f(1)) + \frac{B_2}{2!}(f'(0) - f'(1))\\ &= \frac{1}{2} (f(0) + f(1)) + \frac{1}{12}(f'(0) - f'(1)) \end{split}\]

Sei \([a,b] \subset \R\) nun ein beliebiges Intervall. Wir führen nun eine Variablentransformation mit einer Funktion \(\varphi \colon [0,1] \rightarrow [a,b]\) und \(\varphi(t) \coloneqq t\cdot h + a\) durch, wobei \(h \coloneqq b -a\) die Breite des Intervalls \([a,b] \subset \R\) bezeichnet. Dann gilt

\[\varphi(0) \, = \, 0\cdot h + a \, = \, a, \quad \varphi(1) \, = \, 1 \cdot h + a \, = \, b, \quad \varphi'(t) \, = \, h.\]

Basierend auf der Approximationsregel (6.13) können wir mittels Integration durch Substitution herleiten, dass für eine beliebige Funktion \(f \in C^1([a,b])\) gilt

\[\begin{split} \int_a^b f(x) \, \mathrm{d}x \ &= \ \int_{\varphi(0)}^{\varphi(1)} f(x) \, \mathrm{d}x \ = \ \int_0^1 f(t\cdot h + a) \cdot \underbrace{\varphi'(t)}_{=h} \, \mathrm{d}t \\ &= \ h \cdot \left( \frac{1}{2}(f(a) + f(b)) + \frac{1}{12}(h\cdot f'(a) - h \cdot f'(b))\right)\\ &= \ \frac{h}{2}(f(a) + f(b)) + \frac{h^2}{12}(f'(a) - f'(b)) \ =: \ M(h). \end{split}\]

Man beachte, dass der zusätzliche Faktor \(h\) als innere Ableitung von \(f'(th+a)\) auftaucht.

Mit Hilfe der Peanoschen Fehlerdarstellung in [FH07] lässt sich zeigen, dass für den numerischen Approximationsfehler der Integrationsregel \(M(h)\) für eine Funktion \(C^4([a,b])\) gilt:

\[\int_a^b f(x) \, \mathrm{d}x - M(h) \ = \ \frac{h^5}{720} f^{(4)}(\xi), \qquad \xi \in [a,b].\]

Somit liegt die Fehlerordnung der numerischen Integrationsformel \(M(h)\) in der Größenordnung der Simpsonregel, obwohl nur Funktionsauswertungen und Ableitungen am Rand des Intervalls \([a,b] \subset \R\) verwendet werden.

6.2.2. Romberg-Verfahren

Wir wollen zunächst das bestimmte Integral einer Funktion \(f \in C^{2m+2}([0,n])\) auf einem Intervall \([0,n] \subset \R\) für \(n \in \N_+\) mit Hilfe der Euler-Maclaurinschen Summenformel approximieren. Dieses zerlegen wir in \(n\) Teilintervalle der Länge \(1\) und definieren eine passende Folge von Transformationen \(\varphi_i \colon [0,1] \rightarrow [i, i+1], i = 0, \ldots, n-1\) durch \(\varphi_i(t) \coloneqq i + t = x\) betrachten, für die gilt:

\[\varphi_i(0) \ = \ i, \quad \varphi_i(1) \ = \ i+1, \quad \varphi'_i(t) = 1, \qquad i=0,\ldots,n-1.\]

Nun können wir das ursprüngliche bestimmte Integral umschreiben zu:

\[\int_0^n f(x) \, \mathrm{d}x \ = \ \sum_{i=0}^{n-1} \int_i^{i+1} f(t) \, \mathrm{d}t \ = \ \sum_{i=0}^{n-1} \int_0^1 f(i + t) \, \mathrm{d}t.\]

Nun lässt sich für jeden Summanden die Euler-Maclaurinschen Summenformel in Satz 6.3 anwenden, so dass wir insgesamt erhalten

\[\begin{split} \int_0^n &f(x) \, \mathrm{d}x \ = \ \sum_{i=0}^{n-1} \int_0^1 f(i + t) \, \mathrm{d}t \ = \\ & \sum_{i=0}^{n-1} \left( \frac{f(i)}{2} + \frac{f(i+1)}{2} + \sum_{k=1}^m \frac{B_{2k}}{(2k)!} \left( f^{(2k-1)}(i) - f^{(2k-1)}(i+1)\right) - \frac{B_{2m+2}}{(2m+2)!}f^{(2m+2)}(i + \xi_i) \right) %\frac{f(0)}{2} &+ f(1) + f(2) + \ldots + f(n-1) + \frac{f(n)}{2} \\ %&+ \sum_{k=1}^m \frac{B_{2k}}{(2k)!}\left(f^{(2k-1)}(0) - f^{(2k-1)}(n)\right) - n \cdot \frac{B_{2m+2}}{(2m+2)!}f^{(2m+2)}(\xi). \end{split}\]

Wir erkennen, dass sich die Terme in der Differenz durch die Summation praktischerweise wegheben, bis auf die beiden Randterme. Die \(\xi_i \in [0,1]\) hängen vom \(i\)-ten Teilintervall ab und da \(f^{2m+2}\) nach Voraussetzung eine stetige Funktion ist lässt sich auf Grund des Zwischenwertsatzes ein \(\xi \in [0,n]\) finden, so dass für den Mittelwert der Funktionswerte gilt:

\[\frac{1}{n} \sum_{i=0}^{n-1} f^{(2m+2)}(\xi_i) \, = \, f^{(2m+2)}(\xi) \quad \Rightarrow \quad \sum_{i=0}^{n-1} f^{(2m+2)}(\xi_i) \, = \, n f^{(2m+2)}(\xi).\]

Damit erhalten wir insgesamt für ein \(\xi \in [0,n]\) die folgende Darstellung der Euler-Maclaurinschen Summenformel:

\[\begin{split} \int_0^n f(x) \, \mathrm{d}x \ = \ \frac{f(0)}{2} &+ f(1) + f(2) + \ldots + f(n-1) + \frac{f(n)}{2} \\ &+ \sum_{k=1}^m \frac{B_{2k}}{(2k)!}\left(f^{(2k-1)}(0) - f^{(2k-1)}(n)\right) - n \cdot \frac{B_{2m+2}}{(2m+2)!}f^{(2m+2)}(\xi). \end{split}\]

Für ein beliebiges Intervall \([a,b] \subset \R\) mit äquidistanten Stützpunkten \(x_i = a + ih, i=0,\ldots,n\) mit Schrittweite \(h=\frac{b-a}{n}\) und einer Funktion \(f \in C^{2m+2}[a,b])\) erhalten wir nun durch Variablentransformation mit \(\varphi \colon [0,n] \rightarrow [a,b]\) und \(\varphi(x) \ = \ t h + a\) die Darstellung

\[\begin{split} \int_a^b f(x) \, \mathrm{d}x \ = \ &\overbrace{h\cdot(\frac{f(a)}{2} + f(a+h) + f(a+2h) + \ldots + f(a+(n-1)h) + \frac{f(b)}{2})}^{= \, T_1(h)} \\ &+ \sum_{k=1}^m h^{2k}\frac{B_{2k}}{(2k)!}\left(f^{(2k-1)}(a) - f^{(2k-1)}(b)\right) - h^{2m+2} \cdot \frac{B_{2m+2}}{(2m+2)!} (b-a) f^{(2m+2)}(\xi). \end{split}\]

Hierbei bezeichnet \(T_1(h) := T(h)\) die zusammengesetzte Trapezregel aus Stückweise interpolatorische Quadratur mit

\[T(h) \ \coloneqq \ \frac{h}{2} \left(f(a) + 2\sum_{i=1}^{n-1} f(x_i) + f(b) \right).\]

Stellen wir diese Darstellung des Integrals nach \(T_1(h)\) um, so erhalten wir

(6.14)\[T_1(h) \ = \ \int_a^b f(x) \, \mathrm{d}x + \sum_{k=1}^m c_{2k} h^{2k} + c_{2m+2} (b-a) f^{(2m+2)}(\xi)h^{2m+2},\]

wobei die Konstanten \(c_k \in \R\) definiert sind als \(c_{2k} \coloneqq \frac{B_{2k}}{(2k)!}\left(f^{(2k-1)}(b) - f^{(2k-1)}(a)\right)\) für \(k=1,\ldots,m+1\).

Folgendes Korollar bemerkt eine spezielle Eigenschaft der Trapezsumme für periodische Funktionen.

Korollar 6.3 (Trapezsumme für periodische Funktionen)

Sei \(f \in C^{2m+2}(\R)\) eine \(2\pi\)-periodische Funktion, d.h., es gilt \(f^{(2k)}(a) = f^{(2k)}(a+2\pi)\) für \(k=0,\ldots,m\).

Dann ist die Trapezsumme \(T(h)\) für eine feste Schrittweite \(h = \frac{2\pi}{n}\) und einen Startpunkt \(a \in \R\) eine numerische Approximation des bestimmten Integrals von \(f\) von Ordnung \(\mathcal{O}(h^{2m+2})\), d.h.

\[T(h) \ = \ \int_a^{a+2\pi} f(x) \, \mathrm{d}x + \mathcal{O}(h^{2m+2}).\]

Es lässt sich sogar zeigen, dass für jede Funktion \(f \in C^\infty(\R)\) gilt:

\[\left\vert \int_a^{a+2\pi} f(x) \, \mathrm{d}x - T(h) \right\vert \ \overset{h\rightarrow 0}{\longrightarrow} \ 0,\]

schneller als jede Potenz von \(h\). Wir erkennen also, dass sich periodische, glatte Funktionen außerordentlich gut mit der zusammengesetzten Trapezregel integrieren lassen. Diese vereinfacht sich durch die Periodizität in diesem Fall zu:

\[T(h) \ = \ h \cdot \left( \frac{f(a)}{2} + \sum_{i=1}^{n-1} f(a + ih) + \underbrace{\frac{f(a+2\pi)}{2}}_{= \, f(a)} \right) \ = \ h \sum_{i=0}^{n-1} f(a + ih).\]

Bisher haben wir eine Diskretisierung des Intervalls \([a,b] \subset \R\) mit fester Schrittweite \(h > 0\) und \(n \in \N_+\) Stützpunkten betrachtet, für die gilt

\[h \, \coloneqq \, \frac{b-a}{n}, \quad x_i \, \coloneqq \, a + ih, \qquad i=0,\ldots,n.\]

In diesem Abschnitt wollen wir Verfahren für die numerische Integration herleiten, die unterschiedliche Folgen von Schrittweiten \(h_1 > h_2 > \ldots > h_k > 0\) kombinieren, um somit eine hohe Approximationsgenauigkeit zu erhalten.

Wir bezeichnen im Folgenden das bestimmte Integral der Funktion \(f \in C^{2m+2}([a,b])\) mit

\[I \ \coloneqq \ \int_a^b f(x) \, \mathrm{d}x.\]

Sei die Schrittweite \(h \coloneqq b-a\) zunächst als die Breite des Intervalls gewählt. Dann gilt mit der Darstellung der Trapezsumme aus (6.14), dass gilt:

\[T_1(h) \ = \ I + c_1h^2 + c_2h^4 + \ldots + c_m h^{2m} + \mathcal{O}(h^{2m+2}).\]

Identitäten dieser Form nennt man auch eine Entwicklung von \(T_1\) nach den Potenzen von \(h\).

Wenn wir nun die Anzahl der Teilintervalle verdoppeln, das heißt anstatt \(n\in \N_+\) verwenden wir \(2n \in \N_+\) viele Teilintervalle für die Diskretisierung von \([a,b] \subset \R\), so erhalten wir für die Trapezsumme die Entwicklung

\[\begin{split} T_1\left(\frac{h}{2}\right) \ &= \ I + c_1\left(\frac{h}{2}\right)^2 + c_2\left(\frac{h}{2}\right)^4 + \ldots + c_m \left(\frac{h}{2}\right)^{2m} + \mathcal{O}(h^{2m+2}) \\ &= \ I + c_12^{-2}h^2 + c_22^{-4}h^4 + \ldots + c_m 2^{-2m}h^{2m} + \mathcal{O}(h^{2m+2}). \end{split}\]

Die Idee des sogenannten Romberg-Verfahrens ist es nun, durch eine geschickte Linearkombination von \(T_1(h)\) und \(T_1(\frac{h}{2})\) den ersten Term \(c_1h^2\) verschwinden zu lassen und somit ein Verfahren der Ordnung \(\mathcal{O}(h^4)\) zu erhalten. Hierzu bestrachtet man nun die folgende Differenz:

\[2^2\cdot T_1\left(\frac{h}{2}\right) - T_1(h) \ = \ (2^2 - 1)I + c_2(2^{-2} -1)h^4 + \ldots + c_m(2^{2-2m} - 1)h^{2m} + \mathcal{O}(h^{2m+2})\]

Dies können wir wiederum nach dem bestimmten Integral \(I\) umstellen und erhalten so

\[I \ = \ \frac{1}{2^2-1}(2^2T_1\left(\frac{h}{2}\right) - T_1(h)) - c_2\frac{2^{-2}-1}{2^2-1}h^4 - \ldots - c_m \frac{2^{2-2m}-1}{2^2-1}h^{2m} + \mathcal{O}(h^{2m+2}).\]

Wir erhalten also durch Linearkombination zweier zusammengesetzter Trapezregeln mit unterschiedlicher Schrittweite ein Verfahren höherer Ordnung, nämlich

\[T_2(h) \ \coloneqq \frac{1}{2^2-1}\left[2^2 \cdot T_1\left(\frac{h}{2}\right) - T_1(h)\right].\]

Durch sukzessives Anwenden dieser Idee lassen sich Formeln für die numerische Integration von noch höherer Ordnung herleiten. Sie hierzu im Allgemeinen \(T_k(h)\) eine Formel der Ordnung \(\mathcal{O}(h^{2k})\). Dann betrachten wir

\[\begin{split} T_k(h) \ &= \ I + c_kh^{2k} + c_{k+1}h^{2k+2} + \ldots + c_m h^{2m} + \mathcal{O}(h^{2m+2}),\\ T_k\left(\frac{h}{2}\right) \ &= \ I + 2^{-2k}\cdot c_k h^{2k} + \ldots + 2^{-2m} \cdot c_m h^{2m} + \mathcal{O}(h^{2m+2}). \end{split}\]

Durch passende Linearkombination erhalten wir wiederum

\[2^{2k}\cdot T_k\left(\frac{h}{2}\right) - T_k(h) \ = \ (2^{2k}-1) \cdot I + (2^{-2} - 1) \cdot c_{k+1}h^{2k+2} + \ldots + (2^{2k-2m} - 1)\cdot c_m h^{2m} + \mathcal{O}(h^{2m+2}).\]

Mit

\[T_{k+1}(h) \ \coloneqq \ \frac{1}{2^{2k}-1}\left[ 2^{2k} \cdot T_k \left(\frac{h}{2} \right) - T_k(h) \right]\]

erhalten wir also eine numerische Approximation des bestimmten Integrals durch

\[I \ = \ T_{k+1}(h) + \mathcal{O}(h^{2k+2}).\]

Die rekursive Abhängigkeit dieser Formeln lassen sich sehr übersichtlich in einem sogenannten Romberg-Schema darstellen wie in Tab. 6.2 illustriert wird.

Tab. 6.2 Illustration der rekursiven Abhängigkeit von numerischen Integrationsverfahren basierend auf der Trapezsumme mit unterschiedlichen Genauigkeiten in einem Romberg-Schema.

\(h\)	\(T_1(h)\)
		\(\shortarrow{7}\)
\(\frac{h}{2}\)	\(T_1\left(\frac{h}{2}\right)\)	\(\shortarrow{0}\)	\(T_2(h)\)
		\(\shortarrow{7}\)		\(\shortarrow{7}\)
\(\frac{h}{4}\)	\(T_1\left(\frac{h}{4}\right)\)	\(\shortarrow{0}\)	\(T_2\left(\frac{h}{2}\right)\)	\(\shortarrow{0}\)	\(T_3(h)\)
		\(\shortarrow{7}\)		\(\shortarrow{7}\)		\(\shortarrow{7}\)
\(\frac{h}{8}\)	\(T_1\left(\frac{h}{8}\right)\)	\(\shortarrow{0}\)	\(T_2\left(\frac{h}{4}\right)\)	\(\shortarrow{0}\)	\(T_3\left(\frac{h}{2}\right)\)	\(\shortarrow{0}\)	\(T_4(h)\)

Im folgenden Beispiel wenden wir das Romberg-Verfahren zur numerischen Approximation eines bestimmten Integrals an und vergleichen die Genauigkeit der Integrationsformeln \(T_k(h)\) für unterschiedliche \(k \in \N\).

Beispiel 6.7 (Romberg-Integrationsverfahren)

Es sei \(f(x) \coloneqq e^x\) und wir wollen das bestimmte Integral

\[I \ \coloneqq \ \int_0^1 f(x) \, \mathrm{d}x \ \approx \ 1.718281828\]

mit Hilfe des Romberg-Integrationsverfahrens für unterschiedliche Integrationsformeln \(T_k(h)\) mit \(k = 1,\ldots,4\) berechnen.

Tragen wir die Ergebnisse in eine Tabelle ein, so erhalten wir:

\(h\)	\(T_1\)	\(T_2\)	\(T_3\)	\(T_4\)
\(1\)	\(1.859140914\)
\(\frac{1}{2}\)	\(1.753931092\)	\(1.718861151\)
\(\frac{1}{4}\)	\(1.727221904\)	\(1.718318841\)	\(1.718282687\)
\(\frac{1}{8}\)	\(1.720518592\)	\(1.718284155\)	\(1.718281842\)	\(1.718281829\)

Bemerkung 6.8 (Auslöschung beim Romberg-Verfahren)

Da die Trapezsummen \(T_k(h)\) und \(T_k(\frac{h}{2})\) beide für große \(k >> 1\) und kleine Schrittweiten \(h\) jeweils gute Approximationen für das bestimmte Integral \(I = \int_a^b f(x) dx\) liefern, kommt bei der Linearkombination dieser Formeln zu numerischen Rundungsfehlern durch Auslöschung (siehe Rundungsfehler und Gleitkommaarithmetik). Daher lohnt es sich im Allgemeinen nicht über \(k=6\) hinaus die Schrittweiten zu verfeinern.

Alternativ lässt sich anstatt der ursprünglichen Folge von Schrittweiten

\[h_0 = b - a, \quad h_1 = \frac{h_0}{2}, \quad \ldots, \quad h_k = \frac{h_{k-1}}{2}, \qquad k = 2, 3, \ldots\]

aus dem Romberg-Verfahren zu verwenden, kann man die langsam fallendere Bulirsch-Folge wie folgt verwenden:

\[h_0 = b - a, \quad h_1 = \frac{h_0}{2}, \quad h_2 = \frac{h_0}{3}, \quad \ldots, \quad h_k = \frac{h_{k-2}}{2}, \quad h_{k+1} = \frac{h_{k-2}}{3} \qquad k = 3, 5, \ldots\]

Betrachten wir die zusammengesetzte Trapezregel aus Stückweise interpolatorische Quadratur nochmal genauer, so stellt sich heraus, dass diese eine sehr praktische Eigenschaft für die numerische Berechnung des Integrals besitzt. Hat man nämlich bereits für eine Funktion \(f \in C([a,b])\) eine Approximation \(T(h)\) des bestimmten Integrals \(\int_a^b f(x) \mathrm{d}x\) mittels der zusammengesetzten Trapezregel ermittelt und ist mit der Genauigkeit noch nicht zufrieden, so kann man bei einer Verdopplung der Teilintervalle von \([a,b]\) auf die vorangegangene Berechnung zurückgreifen für die Berechnung der neuen Approximation \(T(\frac{h}{2})\), denn es gilt mit \(h \coloneqq \frac{b-a}{n}\) für \(n\in\N\):

\[\begin{split} T\left(\frac{h}{2}\right) \ &= \ \sum_{i=0}^{2n-1} \frac{h}{4} (f(x_i) + f(x_{i+1})) \\ &= \ \frac{1}{2} \underbrace{\sum_{i=0}^{n-1} \frac{h}{2}(f(x_{2i}) + f(x_{2i+2}))}_{= \, T(h)} \, + \, \sum_{i=1}^{n-1} \frac{h}{2}(f(x_{2i-1}) + f(x_{2i+1})) \\ &= \ \frac{T(h)}{2} + \sum_{i=1}^{n-1} \frac{h}{2}(f(x_{2i-1}) + f(x_{2i+1})). \end{split}\]

Diese Beobachtung ist einer der Gründe, warum das oben eingeführte Romberg-Verfahren numerisch effizient berechnet werden kann.