7.1. Potenzmethode und inverse Iteration

Wir beginnen mit einer Methode zur Berechnung des größten Eigenwerts einer Matrix \(A\), die sogenannte Potenzmethode oder Vektoriteration. Betrachten wir dazu zunächst eine symmetrische Matrix \(A \in \mathbb{R}^{n \times n}\), dann können wir die Diagonalisierung \(A=V \Lambda V^T\) verwenden. Hier ist \(V\) eine orthogonale Matrix, deren Spalten die Eigenvektoren von \(A\) sind, und \(\Lambda\) ist eine Diagonalmatrix bestehend aus den Eigenwerten. Berechnen wir für ein \(x^0\) die Anwendung \(A x^0 = V D V^T x^0\), so können wir dies als

\[A x^0 = \sum_{j=1}^n \lambda_j v_j (v_j^T x^0)\]

schreiben und sehen, dass die Komponenten von \(x_0\) bezüglich der Orthonormalbasis \((v_j)\) mit \(\lambda_j\) verstärkt werden, am meisten natürlich der zum größten Eigenwert gehörige Anteil. Dies induziert die Idee einfach immer wieder mit der Matrix \(A\) zu multiplizieren, um am meisten den Anteil zum größten Eigenwert zu verstärken. Um keine Divergenz zu erhalten, muss dann natürlich noch normiert werden. Diese Idee lässt sich auf allgemeine Matrizen übertragen und führt auf die sogenannte Potenzmethode.

Algorithmus 7.1 (Potenzmethode)

Für eine Matrix \(A\in \C^{n\times n}\) und gegebener Anfangsvektor \(x_0\in\C^n\) ist die Potenzmethode oder Vektoriteration durch die Vorschrift

\[x^{k+1} = \frac{1}{\norm{Ax^k}} Ax^k.\]

gegeben.

Wir zeigen im Folgenden, dass die Potenzmethode tatsächlich einen Eigenwert zum größten Eigenvektor liefert. Wir nutzten im folgenden eine Zerlegung des Raums in die Eigenvektoren \(v_1,\ldots, v_n\), s.d. sich der Startvektor durch

\[\begin{aligned} x^0 = \sum_{i=1}^{n} \alpha_i v_i \end{aligned}\]

ausdrücken lässt. Hierbei, gehen wir davon aus, dass

(7.1)\[\begin{aligned} \alpha_1\neq 0 \end{aligned}\]

gilt, also dass der Anteil zum betragsmäßig größten Eigenwert nicht null ist.

Lemma 7.1 (Konvergenz der Potenzmethode)

Es sei \(A\in\C^{n\times n}\) eine Matrix mit Eigenwerten \(\lambda_1,\ldots,\lambda_n\in\C\) mit \(\abs{\lambda_1}> \abs{\lambda_2} \geq \abs{\lambda_3} \geq \ldots \geq \abs{\lambda_n}\). Zu einem gegebenen Startvektor \(x_0\in\C^n\) der (7.1) erfüllt konvergiert die Vektoriteration in Algorithmus 7.1 gegen einen Eigenvektor zum Eigenwert \(\lambda_1\).

Proof. Wir gehen vereinfachend von einer reell diagonalisierbaren Matrix \(A\in\R^{n\times n}\) aus, der allgemeine Fall lässt sich analog mit der Jordanschen Normalform zeigen. In diesem Fall existiert für \(\Lambda = \text{diag}(\lambda_1,\ldots,\lambda_n)\) eine Matrix \(V = (v_1|\ldots|v_n)\), wobei \(v_i\in\R^n\) ein Eigenvektor zum Eigenwert \(\lambda_i\) ist, s.d.

\[\begin{aligned} A = V \Lambda V^{-1}. \end{aligned}\]

Insbesondere bilden die \(v_i\) eine Basis des \(\R^n\) und somit existieren Koeffizienten \(\alpha_i\), s.d. \(x^0 = \sum_{i=1}^n \alpha_i v_i\). Für die \(k\)-te Iterierte der Potenzmethode haben wir

\[\begin{aligned} x^{k+1} = \frac{\norm{A^k x^0}} A^k x^0 \end{aligned}\]

wobei wir sehen, dass

\[\begin{aligned} A^k x_0 &= (V\Lambda V^{-1})^k x_0 = V \Lambda^k V^{-1} x_0 \\&= (V\Lambda^k) \sum_{i=1}^n \alpha_i V^{-1} v_i \\&= (V \Lambda^k) \sum_{i=1}^n \alpha_i e_i \\&= V \lambda_1^k \left(\alpha_1 e_1 + \sum_{i=2}^n \alpha_i \left(\frac{\lambda_i}{\lambda_1}\right)^k e_i\right) \\&= \alpha_1 \lambda_1^k v_1 + \sum_{i=2}^n \alpha_i \left(\frac{\lambda_i}{\lambda_1}\right)^k v_i \end{aligned}\]

Wegen \(\left(\frac{\lambda_i}{\lambda_1}\right)^k \to 0\) für \(k\to\infty, i>1\) folgt dann

\[\begin{aligned} \frac{1}{\norm{A^k x^0}} A^k x_0 \to \frac{1}{\norm{v_1}} v_1 \end{aligned}\]

für \(k\to\infty\). ◻

Bemerkung 7.1

Um z.B. den Eigenvektor zum zweitgrößten Eigenwert zu berechnen müsste beim Startwert in (7.1) \(\alpha_1=0, \alpha_2\neq0\) gelten. Falls \(A\) eine symmetrische Matrix ist könne wir dazu \(x^0\) orthogonal zu \(v_1\) wählen. Mit dieser Strategie können wir alle Eigenvektoren berechnen.

Um den Eigenwert zu berechnen betrachtet man den sogenannten Rayleigh-Quotienten

\[\begin{aligned} \lambda_1^k := \frac{(x^k)^T A x^k }{(x^k)^T x^k} \end{aligned}\]

wofür aus Lemma 7.1 folgendes Korollar erhalten.

Korollar 7.1

Unter den Voraussetzungen von Lemma 7.1 konvergiert der Rayleigh-Quotient gegen den betragsmäßig größten Eigenwert \(\lambda_1\).

Beispiel 7.3

Wir betrachten die Matrix

\[\begin{aligned} A= \begin{pmatrix} 1 & 2\\ 1 & 1 \end{pmatrix} \end{aligned}\]

und wenden darauf die Potenzmethode an. Die ersten vier Iterationen sind in Abb. 7.1 visualisiert.

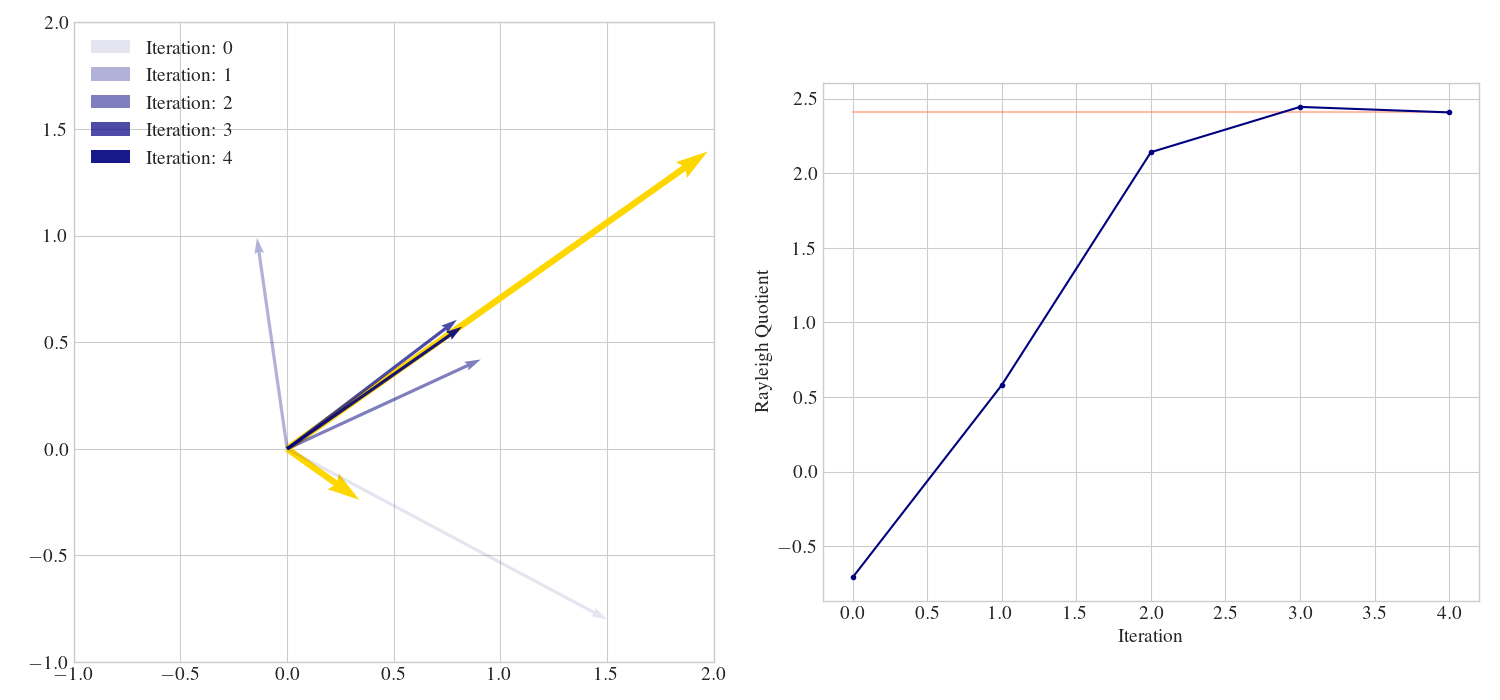
Abb. 7.1 Die ersten vier Iterationen der Potenzmethode aus Beispiel 7.3 in blau. In gelb sind die Eigenvektoren skalirt mit den Eigenwerten dargestellt. Im rechten Plot ist das verhalten des Rayleigh-Quotienten abgebildet, wobei der eigentliche Wert des größten Eigenwerts in hell-rot dargestellt ist.

Wollen wir direkt einen anderen Eigenwert von \(A\) berechnen, so kann dazu die inverse Iteration genutzt werden. Grundlage dafür ist folgendes Resultat.

Lemma 7.2

Seien \(A \in \mathbb{C}^{n \times n}\) und \(\lambda \in \mathbb{C}\) gegeben. Sei \(\lambda_i\) ein Eigenwert von \(A\) mit minimalem Abstand zu \(\lambda\), d.h.

\[\vert \lambda_i - \lambda \vert \leq \vert \lambda_j - \lambda \vert\]

für alle Eigenwerte \(\lambda_j\) von \(A\). Dann ist \((\lambda - \lambda_i)^{-1}\) ein betragsmäßig größter Eigenwert von

\[B = (\lambda I - A)^{-1}.\]

Proof. Beweis. Wir sehen sofort, dass \(\mu_j\) ein Eigenwert von \(B\) mit Eigenvektor \(x_j\), wenn \(\lambda_j = \lambda - \frac{1}{\mu_j}\) ein Eigenwert von \(A\) mit dem selben Eigenvektor ist und umgekehrt. Die Eigenwerte von \(B\) sind also \(\frac{1}{\lambda - \lambda_j}\) und dies ist betragsmässig maximal, wenn \(\vert \lambda- \lambda_j\vert\) minimal ist. ◻

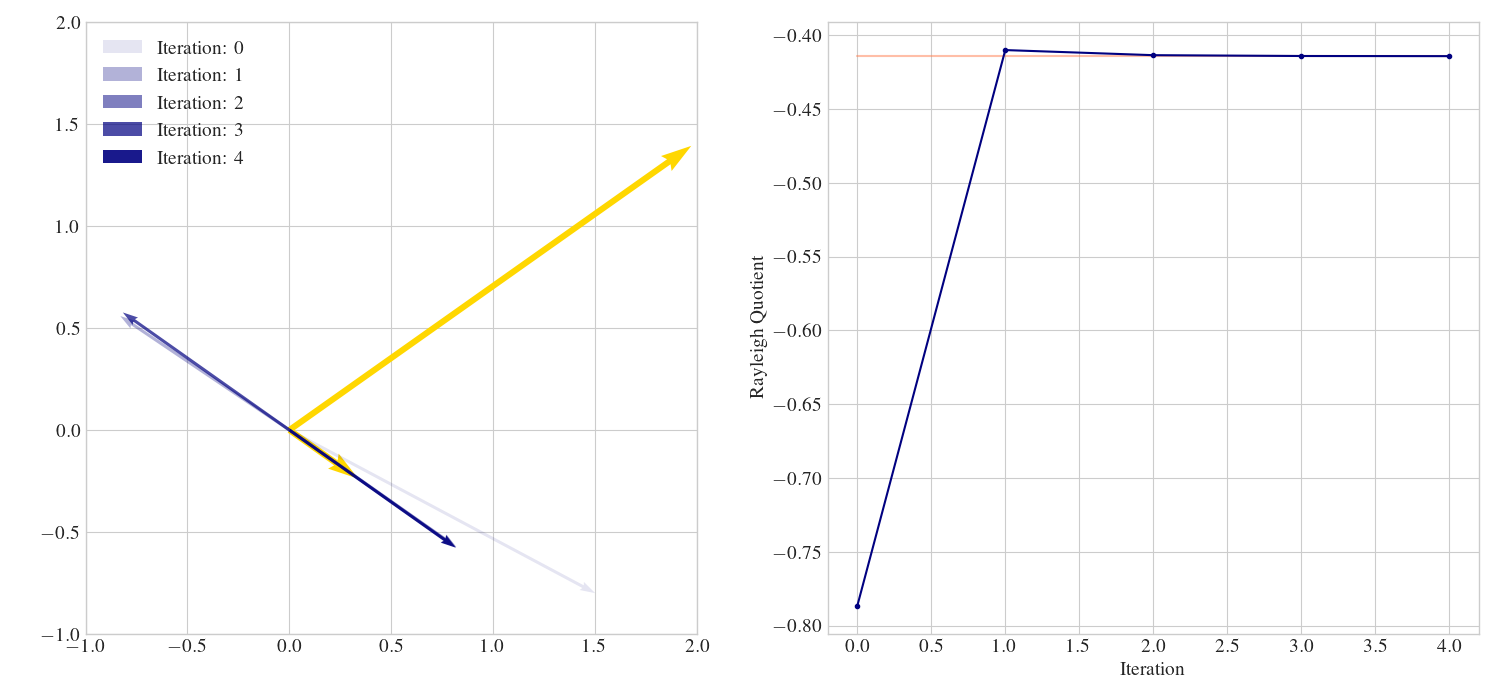
Abb. 7.2 Die inverse Iteration für die Matrix aus Beispiel 7.3 mit \(\lambda=-1\).

Damit sehen wir, dass die Iteration

\[x^{k+1} = \frac{1}{\Vert y^k \Vert}y^k , \qquad y^k = (\lambda I - A)^{-1}x^k\]

unter analogen Bedingungen gegen einen Eigenvektor zum Eigenwert \(\frac{1}{\lambda - \lambda_j}\) konvergiert, wobei \(\lambda_i\) der zu \(\lambda\) nächstgelegene Eigenwert ist. Die Matrix dabei ist auch invertierbar, falls \(\lambda\) kein Eigenwert ist, in diesem Fall wären wir ohnehin schon im ersten Schritt fertig. Um ein effizientes Verfahren zu erhalten, sollte man für großes \(n\) natürlich die Berechnung der inversen Matrix vermeiden und statt dessen in jedem Schritt das lineare Gleichungssystem

\[\lambda y^k - A y^k = x^k\]

lösen. Hat man eine hinreichend gute Näherung für den Eigenvektor \(x^k\), kann eine Approximation des Eigenwertes mithilfe eines modifizierten Rayleigh-Quotienten berechnet werden. Denn aus

\[\frac{1}{\lambda - \lambda_j} \approx \mu_j^k =: \frac{(x^k)^T (\lambda I - A)^{-1} x^k }{(x^k)^T x^k}\]

folgt sofort \(\lambda_j \approx \lambda - \frac{1}{\mu_j^k}\).